Учет массы упругой системы при колебаниях.
Если колеблющаяся система, несущая груз Q, обладает довольно значительной распределенной массой (число степеней свободы, следовательно, велико), то упрощенные расчеты, будут иметь уже значительную погрешность. В этом случае дифференциальные уравнения движения составляются с учетом массы системы. При решении подобного рода задач удобнее исходить не из условий равновесия, а из закона сохранения энергии.
Полагая, что количество энергии, сообщенное системе при выведении ее из положения равновесия и представляющее собой сумму кинетической и потенциальной энергии груза и упругой системы, при свободных колебаниях остается постоянным, получаем уравнение
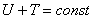
| (4) |
Это уравнение показывает, что при колебаниях происходит непрерывный процесс преобразования энергии из одного вида в другой, не сопровождающийся какими-либо потерями энергии. Когда упругая система достигает одного из крайних положений, в котором скорость колебательного движения равна нулю, а следовательно, равна нулю и кинетическая энергия (T=0), потенциальная энергия груза и системы достигает наибольшего значения 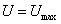 ; наоборот, в положении равновесия
; наоборот, в положении равновесия 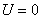 и
и 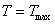 .
.
Заметим, что принцип, положенный в основу этого уравнения, применим лишь для систем с одной степенью свободы, так как закон сохранения энергии не учитывает обмена энергии, происходящего в системах с несколькими степенями свободы. Таким образом, решение задачи о колебаниях системы с большим числом степеней свободы здесь сводится к простейшей задаче и мы сможем приближенно найти лишь одну (первую) частоту свободных колебаний.
Рассмотрим теперь некоторые примеры использования исходного уравнения.
В качестве первого примера исследуем колебания груза Q, подвешенного к нижнему концу призматического стержня длиной l, площадью поперечного сечения F и удельным весом 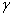 (Рис. 4). Выведенный из положения равновесия и затем предоставленный самому себе груз начнет совершать продольные колебания около положения равновесия. Составим выражения для U и Т колеблющейся системы: груз — стержень.
(Рис. 4). Выведенный из положения равновесия и затем предоставленный самому себе груз начнет совершать продольные колебания около положения равновесия. Составим выражения для U и Т колеблющейся системы: груз — стержень.
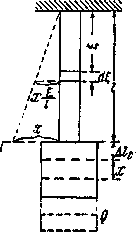
Рис.4. Расчетная схема колебаний подвешенного груза
Потенциальная энергия системы по сравнению с положением равновесия изменится на 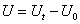 , где
, где 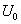 — потенциальная энергия системы в начальный момент (в положении равновесия), a
— потенциальная энергия системы в начальный момент (в положении равновесия), a 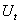 — в момент t.
— в момент t.
Потенциальную энергию груза Q в начальный момент обозначим через 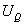 ; потенциальная энергия стержня в тот же момент равна
; потенциальная энергия стержня в тот же момент равна 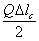 , где
, где 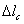 — статическая деформация стержня от груза Q.
— статическая деформация стержня от груза Q.
Таким образом,
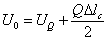
В момент t, когда груз переместится на расстояние х и стержень получит такую же дополнительную деформацию х, потенциальная энергия груза уменьшится на Qx, а сила упругого сопротивления стержня и статическая деформация его увеличатся в отношении 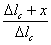 . Поэтому
. Поэтому
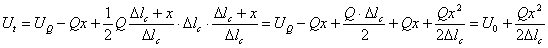
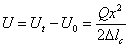
| (5) |
Кинетическая энергия системы складывается из кинетической энергии груза 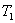 и стержня
и стержня 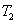 . Кинетическая энергия груза
. Кинетическая энергия груза 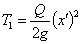 . При вычислении кинетической энергии стержня учтем, что в некоторый момент t скорость груза и нижнего конца стержня равна х', а верхнего — нулю. Скорости промежуточных сечений будут иметь значения, заключающиеся между этими двумя.
. При вычислении кинетической энергии стержня учтем, что в некоторый момент t скорость груза и нижнего конца стержня равна х', а верхнего — нулю. Скорости промежуточных сечений будут иметь значения, заключающиеся между этими двумя.
Предположим, что при колебаниях перемещения всех сечений стержня по отношению к закрепленному концу меняются по тому же закону, что и при статическом растяжении, т. е. пропорционально расстоянию от закрепленного сечения. Таким образом, если нижнее сечение стержня переместилось на величину х, то сечение, отстоящее от места защемления на 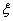 , переместится на величину
, переместится на величину 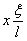 , скорость этого сечения будет равна
, скорость этого сечения будет равна 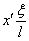 . Живая сила элемента стержня длиной
. Живая сила элемента стержня длиной 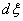 , отстоящего на
, отстоящего на 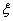 от закрепленного конца, будет равна:
от закрепленного конца, будет равна:
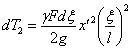
Кинетическая энергия всего стержня будет равна сумме величин 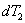 , т.е.
, т.е.
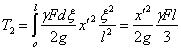
Таким образом, живая сила стержня равна живой силе груза, имеющего массу 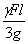 , т. е. равную трети массы стержня, и двигающегося с той же скоростью х', что и груз Q. Полная же кинетическая энергия системы груз — стержень будет:
, т. е. равную трети массы стержня, и двигающегося с той же скоростью х', что и груз Q. Полная же кинетическая энергия системы груз — стержень будет:
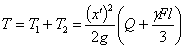
Подставляя Т и выражение U (4) в уравнение (5), дифференцируем последнее по t и находим:
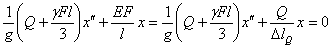
или
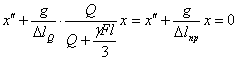
Здесь 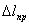 — статическая деформация от груза
— статическая деформация от груза 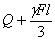 . Полученное дифференциальное уравнение движения с учетом массы колеблющегося стержня отличается от полученного ранее уравнения только величиной множителя при х и полностью совпадает с ним, если пренебречь массой стержня. Поэтому поправка на массу стержня, которую нужно ввести в предыдущие расчеты, состоит в том, что при определении частоты свободных колебаний стержня статическая деформация его вычисляется не от груза Q, но от груза Q, сложенного с одной третью веса стержня. Таким образом, учет массы колеблющегося стержня уменьшает частоту свободных колебаний и увеличивает их период. Величину
. Полученное дифференциальное уравнение движения с учетом массы колеблющегося стержня отличается от полученного ранее уравнения только величиной множителя при х и полностью совпадает с ним, если пренебречь массой стержня. Поэтому поправка на массу стержня, которую нужно ввести в предыдущие расчеты, состоит в том, что при определении частоты свободных колебаний стержня статическая деформация его вычисляется не от груза Q, но от груза Q, сложенного с одной третью веса стержня. Таким образом, учет массы колеблющегося стержня уменьшает частоту свободных колебаний и увеличивает их период. Величину 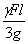 называют приведенной массой стержня.
называют приведенной массой стержня.
Лекция № 49. Расчет динамического коэффициента при ударной нагрузке.
Основные положения
Явление удара получается в том случае, когда скорость рассматриваемой части конструкции или соприкасающихся с ней частей изменяется в очень короткий период времени.
При забивке свай тяжелый груз падает с некоторой высоты на верхний торец сваи и погружает ее в грунт; баба останавливается почти мгновенно, вызывая удар. Аналогичные явления происходят при ковке; удар испытывают и проковываемое изделие и шток молота с бойком, так как последний очень быстро останавливается при соприкосновении с изделием. Во время удара между обеими ударяющимися деталями возникают весьма большие взаимные давления. Скорость ударяющего тела за очень короткий промежуток времени изменяется и в частном случае падает до нуля; тело останавливается. Значит, на него от ударяемой детали передаются очень большие ускорения, направленные в сторону, обратную его движению, т. е. передается реакция 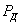 , равная произведению массы ударяющего тела на это ускорение.
, равная произведению массы ударяющего тела на это ускорение.
Обозначая это ускорение через а, можно написать, что реакция 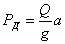 , где Q — вес ударяющего тела. По закону равенства действия и противодействия на ударяемую. часть конструкции передается такая же сила, но обратно направленная (рис.1). Эти силы и вызывают напряжения в обоих телах.
, где Q — вес ударяющего тела. По закону равенства действия и противодействия на ударяемую. часть конструкции передается такая же сила, но обратно направленная (рис.1). Эти силы и вызывают напряжения в обоих телах.

Рис.1. Расчетная схема ударного нагружения.
Таким образом, в ударяемой части конструкции возникают такие напряжения, как будто к ней была приложена сила инерции ударяющего тела; мы можем вычислить эти напряжения, рассматривая силу инерции 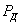 как статическую нагрузку нашей конструкции. Затруднение заключается в вычислении этой силы инерции. Продолжительности удара, т. е. величины того промежутка времени, в течении которого происходит падение скорости до нуля, мы не знаем. Поэтому остается неизвестной величина ускорения а, а стало быть, и силы
как статическую нагрузку нашей конструкции. Затруднение заключается в вычислении этой силы инерции. Продолжительности удара, т. е. величины того промежутка времени, в течении которого происходит падение скорости до нуля, мы не знаем. Поэтому остается неизвестной величина ускорения а, а стало быть, и силы 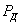 . Таким образом, хотя вычисление напряжений при ударе представляет собой частный случай задачи учета сил инерции, однако для вычисления силы
. Таким образом, хотя вычисление напряжений при ударе представляет собой частный случай задачи учета сил инерции, однако для вычисления силы 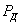 и связанных с ней напряжений и деформаций здесь приходится применять иной прием и пользоваться законом сохранения энергии.
и связанных с ней напряжений и деформаций здесь приходится применять иной прием и пользоваться законом сохранения энергии.
При ударе происходит очень быстрое превращение одного вида энергии в другой: кинетическая энергия ударяющего тела превращается в потенциальную энергию деформации. Выражая эту энергию в функции силы 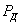 или напряжений, или деформаций получаем возможность вычислить эти величины.
или напряжений, или деформаций получаем возможность вычислить эти величины.
Дата добавления: 2016-03-05; просмотров: 1005;
