Сложение гармонических колебаний
Одинаковых частот
Сложение колебаний одинаковых частот проще всего осуществить с помощью так называемой векторной диаграммы. Построение векторной диаграммы основано на известном факте: проекция результирующего вектора равна сумме проекций слагаемых векторов. Поэтому сложение гармонических колебаний
х1 = a cos(wt + j01) и х2= b cos(wt + j02) (16.16)
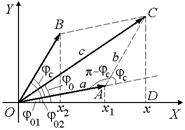 Рис. 16.17
Рис. 16.17
|
осуществляется так. Строят векторы 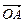 и
и 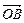 ,изображающие первое и второе колебания (рис. 16.17). Их модули равны амплитудам складываемых колебаний, а угол между ними, равный
,изображающие первое и второе колебания (рис. 16.17). Их модули равны амплитудам складываемых колебаний, а угол между ними, равный
jс = j02 – j01,
представляет собой сдвиг фаз между этими колебаниями.
Так как частоты складываемых колебаний равны, то угол jс между векторами 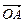 и
и 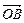 не меняется.
не меняется.
Проекция суммарного вектора 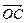 представляет собой результирующее колебание:
представляет собой результирующее колебание:
х = х1 + х2 = сcos(wt + j0). (16.17)
Оно происходит с той же частотой w, что и колебания х1и х2. Модуль с вектора 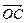 равен амплитуде результирующих колебаний. По теореме косинусов для треугольника ОСА получим
равен амплитуде результирующих колебаний. По теореме косинусов для треугольника ОСА получим
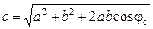 . (16.18)
. (16.18)
Амплитуда результирующего колебания зависит от амплитуд складываемых колебаний а и b и сдвига фаз между ними.
Пример. Найти амплитуду колебания х(t) = x1(t) + x2(t), где x1(t) = Acoswt, x2(t) = Bsinwt, а также сдвиг фаз между колебаниями х1(t) и x2(t).
1. Согласно известной тригонометрической формуле sinwt = 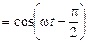 , поэтому x2(t)
, поэтому x2(t) 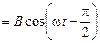 .
.
2. Изобразим на векторной диаграмме первое колебание вектором 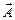 , а второе – вектором
, а второе – вектором 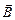 в момент t = 0 (рис. 16.18). (второе колебание отстает от первого на p/2, векторы вращаются против часовой стрелки.) Тогда результирующее колебание изобразится вектором
в момент t = 0 (рис. 16.18). (второе колебание отстает от первого на p/2, векторы вращаются против часовой стрелки.) Тогда результирующее колебание изобразится вектором 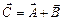 . Модуль этого вектора
. Модуль этого вектора 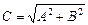 равен амплитуде результирующего колебания х(t), а сдвиг по фазе между векторами
равен амплитуде результирующего колебания х(t), а сдвиг по фазе между векторами 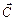 и
и 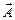 – угол j – легко найти из прямоугольного треугольника, образованного векторами
– угол j – легко найти из прямоугольного треугольника, образованного векторами 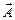 и
и 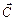 :
:
tgj = 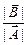 Þ j = arctg
Þ j = arctg 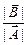 .
.
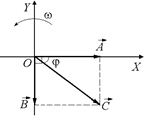 Рис. 16.18
Рис. 16.18
|
Заметим, что поскольку векторы 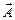 и
и 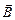 вращаются с одинаковой угловой скоростью w, то их взаимное расположение со временем не меняется. Поэтому и величину С и сдвиг по фазе j можно найти, изобразив векторы
вращаются с одинаковой угловой скоростью w, то их взаимное расположение со временем не меняется. Поэтому и величину С и сдвиг по фазе j можно найти, изобразив векторы 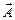 и
и 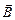 в любой момент времени (рис. 16.19).
в любой момент времени (рис. 16.19).
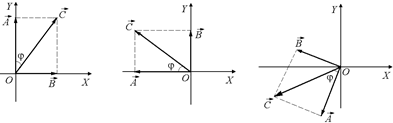
Рис. 16.19
СТОП! Решите самостоятельно: С3.
Построим векторные диаграммы для уже рассмотренных нами простейших цепей переменного тока.
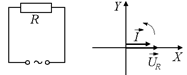 Рис. 16.20
Рис. 16.20
|
В случае на рис. 16.20 ток и напряжение колеблются в одной фазе.
В случае на рис. 16.21 напряжение отстает от тока на p/2.
В случае на рис. 16.22 напряжение опережает ток на p/2.

Рис. 16.21 Рис. 16.22
RL-цепь
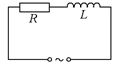 Рис. 16.23
Рис. 16.23
|
Рассмотрим цепь переменного тока, состоящую из последовательно соединенного резистора сопротивлением R и катушки с индуктивностью L (рис. 16.23). Переменное напряжение изменяется по закону u(t) = U0coswt.
Прежде всего заметим, что ток в любой момент времени один и тот же, и изменяется он с той же частотой w, что и напряжение. Кроме того, можно утверждать, что в момент времени t общее напряжение равно сумме напряжений на резисторе и катушке:
u(t) = uR(t) + uL(t).
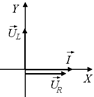 Рис. 16.24
Рис. 16.24
|
Попробуем найти: 1) амплитуду тока I0; 2) амплитуду напряжения на резисторе UR; 3) амплитуду напряжения на катушке UL; 4) сдвиг фаз j (если он есть) между током и общим напряжением; 5) функцию i(t).
Поскольку очевидно, что колебания u(t), u0(t), uс(t) и i(t) происходят с одинаковой циклической частотой w, воспользуемся векторной диаграммой. Сначала изобразим колебания тока вектором 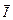 (рис. 16.24). Направим этот вектор горизонтально.
(рис. 16.24). Направим этот вектор горизонтально.
Читатель: Но тогда получается, что i(t) = I0coswt, т.е. начальная фаза тока равна нулю! А откуда мы это знаем?
Автор: А я не утверждаю, что вектор 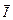 занимает указанное положение в начальный момент времени. Но ведь наверняка в какой-то момент времени он такое положение займет. Вот в этот момент мы его и изобразили. А теперь все остальные векторы пусть под него «подстраиваются».
занимает указанное положение в начальный момент времени. Но ведь наверняка в какой-то момент времени он такое положение займет. Вот в этот момент мы его и изобразили. А теперь все остальные векторы пусть под него «подстраиваются».
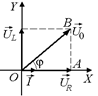 Рис. 16.25
Рис. 16.25
|
Колебания напряжения на резисторе совпадает с током по фазе, поэтому вектор 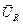 совпадает по направлению с вектором
совпадает по направлению с вектором 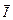 . А вот напряжение на катушке опережает ток на p/2, поэтому вектор
. А вот напряжение на катушке опережает ток на p/2, поэтому вектор 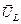 направлен вертикально вверх (см. рис. 16.22). Тогда результирующее напряжение, равное сумме напряжений на катушке и резисторе, будет изображаться вектором
направлен вертикально вверх (см. рис. 16.22). Тогда результирующее напряжение, равное сумме напряжений на катушке и резисторе, будет изображаться вектором 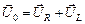 (рис. 16.25).
(рис. 16.25).
По теореме Пифагора из DАОВ имеем:
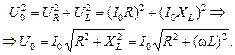
Отсюда
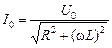 . (16.19)
. (16.19)
Величину
ZRL = 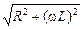 (16.20)
(16.20)
назовем полным сопротивлением RL-цепи. Тогда
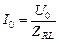 . (16.21)
. (16.21)
Разделив обе части равенства (16.21) на 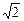 , получим
, получим
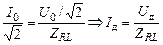 . (16.21а)
. (16.21а)
Воспользуемся законом Ома для амплитудных значений тока и напряжения на сопротивлениях R и ХL:
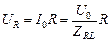 . (16.22)
. (16.22)
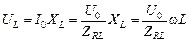 . (16.23)
. (16.23)
Сдвиг по фазе между напряжением и током находим из DОАВ (cм. рис. 16.25):
tgj = 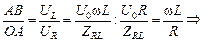
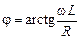 . (16.24)
. (16.24)
Поскольку ток отстает от напряжения на j, то если u(t) = = U0coswt, тогда
i(t) = I0cos(wt – j). (16.25)
Заметим, что сумма действующих значений напряжения на катушке и резисторе не равна общему действующему напряжению, потому что, как легко видеть из DОАВ (см. рис. 16.25), UR + UL > U0, а значит, 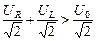 , т.е. URд + ULд > U0д. И это легко понять, если учесть, что напряжения на резисторе и катушке всегда имеют разные фазы (разность фаз всегда равна p/2). Поэтому для действующих значений напряжений справедливо другое соотношение:
, т.е. URд + ULд > U0д. И это легко понять, если учесть, что напряжения на резисторе и катушке всегда имеют разные фазы (разность фаз всегда равна p/2). Поэтому для действующих значений напряжений справедливо другое соотношение:
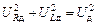 . (16.26)
. (16.26)
Задача 16.7. Когда к катушке подвели постоянное напряжение 10 В, сила тока в катушке была равна 1,0 А. Такая же сила тока протекает по этой катушке, если к ней подвести переменное напряжение 50 В. Какова индуктивность катушки? Как изменится сила тока в каждом из указанных случаев, если из катушки вынуть железный сердечник? Частота тока n = 50 Гц.
| U1 = 10 B I1 = 1,0 A Uд = 50 В Iд = 1,0 А n = 50 Гц | Решение. В первом случае ток постоянный, поэтому
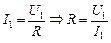 , (1)
R – активное сопротивление катушки.
Во втором случае цепь соответствует схеме, показанной на рис. 16.23: катушку, обладающую актив- , (1)
R – активное сопротивление катушки.
Во втором случае цепь соответствует схеме, показанной на рис. 16.23: катушку, обладающую актив-
|
| L = ? | |
ным сопротивлением R, можно представить как «идеальную» катушку индуктивностью L с нулевым активным сопротивлением, соединенную последовательно с активным сопротивлением R. Тогда по формуле (16.21а)
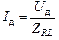 , (2)
, (2)
где по формуле (16.20)
ZRL = 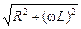 . (3)
. (3)
Подставляя (3) в (2), получим
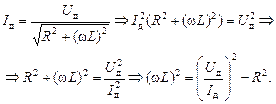
Подставляя R из (1), получим
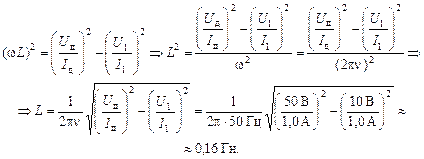
Если из катушки вынуть железный стержень, то в случае постоянного тока – ничего не изменится. В случае переменного тока индуктивность L, а значит, общее сопротивление 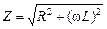 сильно уменьшится, и ток возрастет.
сильно уменьшится, и ток возрастет.
Ответ: 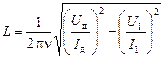 » 0,16 Гн.
» 0,16 Гн.
СТОП! Решите самостоятельно: В23–В25, С7–С9, С15.
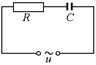 Рис. 16.26
Рис. 16.26
|
RC-цепь
Рассмотрим цепь переменного тока, состоящую из последовательно соединенного резистора сопротивлением R и конденсатора емкостью С (рис. 16.26). Переменное напряжение на выходе изменяется по закону u(t) = U0coswt.
Как и в случае RL-цепи, найдем: 1) амплитуду тока I0; 2) амплитуду напряжения на резисторе UR; 3) амплитуду напряжения на конденсаторе UС; 4) сдвиг фаз j между током и общим напряжением; 5) функцию i(t).
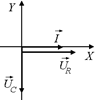 Рис. 16.27
Рис. 16.27
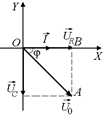 Рис. 16.28
Рис. 16.28
|
Изобразим на векторной диаграмме колебания тока вектором 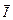 , колебания напряжения на резисторе – вектором
, колебания напряжения на резисторе – вектором 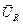 , колебания напряжения на конденсаторе – вектором
, колебания напряжения на конденсаторе – вектором 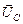 . При этом учтем (см. рис. 16.21), что напряжение на конденсаторе отстает от тока на p/2 (рис. 16.27).
. При этом учтем (см. рис. 16.21), что напряжение на конденсаторе отстает от тока на p/2 (рис. 16.27).
Поскольку в любой момент времени t u(t) = = uR(t) + uC(t), то вектор результирующего напряжения равен 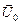 =
= 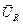 +
+ 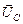 . Из DОАВ (рис. 16.28) по теореме Пифагора получим
. Из DОАВ (рис. 16.28) по теореме Пифагора получим
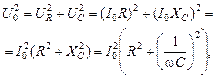
Тогда
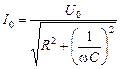 , (16.27)
, (16.27)
или
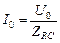 . (16.28)
. (16.28)
Для действующих значений справедливо
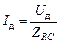 , (16.28а)
, (16.28а)
где ZRC – полное сопротивление RC-цепи:
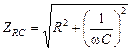 . (16.29)
. (16.29)
Тогда согласно закону Ома
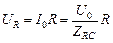 . (16.30)
. (16.30)
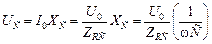 . (16.31)
. (16.31)
Сдвиг по фазе между напряжением и током находим из DОАВ (cм. рис. 16.28):
tgj = 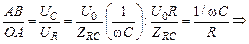
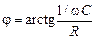 . (16.32)
. (16.32)
Поскольку в данном случае ток опережает напряжение на j, то если u(t) = U0coswt, тогда
i(t) = I0cos(wt + j). (16.33)
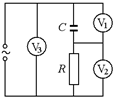 Рис. 16.29
Рис. 16.29
|
Задача 16.8. В цепи переменного тока (рис. 16.29) показания первого и второго вольтметров U1 = 12 В и U2 = 9 В. Каково показание третьего вольтметра?
Решение. Нам надо найти действующее значение результирующего напряжения Uд в RC-цепи. Обозначим значение действующего напряжения на конденсаторе U1, на резисторе – U2, тогда амплитудные значения напряжений на конденсаторе и резисторе равны UC = U1 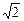 , UR = U2
, UR = U2 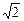 .
.
Амплитудное значение результирующего напряжения (см. рис. 16.28)
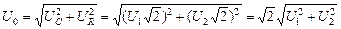 ,
,
а искомое действующее значение общего напряжения (а именно его показывает третий вольтметр) равно
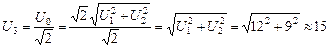 В.
В.
Ответ: 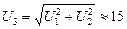 В.
В.
СТОП! Решите самостоятельно: А13, В26, В27.
LC- цепь
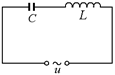 Рис. 16.30
Рис. 16.30
|
Рассмотрим цепь переменного тока, состоящую из последовательно соединенных конденсатора емкостью С и катушки с индуктивностью L (рис. 16.30).
Пусть переменное напряжение в сети изменяется по закону u(t) = U0coswt.
Попробуем найти: 1) амплитуду тока I0; 2) амплитуду напряжения на катушке UL; 3) амплитуду напряжения на конденсаторе UС; 4) сдвиг фаз j между током и общим напряжением; 5) функцию i(t).
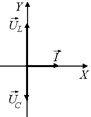 Рис. 16.31
Рис. 16.31
|
Изобразим на векторной диаграмме (рис. 16.31) колебания тока вектором 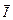 , колебания напряжения на катушке – вектором
, колебания напряжения на катушке – вектором 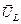 , колебания напряжения на конденсаторе – вектором
, колебания напряжения на конденсаторе – вектором 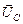 . При этом учтем, что напряжение на катушке опережает ток на p/2 (см. рис. 16.22), а напряжение на конденсаторе отстает от тока на p/2 (см. рис. 16.21).
. При этом учтем, что напряжение на катушке опережает ток на p/2 (см. рис. 16.22), а напряжение на конденсаторе отстает от тока на p/2 (см. рис. 16.21).
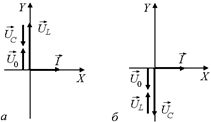 Рис. 16.32
Рис. 16.32
|
Поскольку в любой момент времени t u(t) = uC(t) + uL(t), то вектор результирующего напряжения 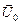 =
= 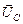 +
+ 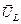 будет либо опережать ток по фазе на p/2, если |
будет либо опережать ток по фазе на p/2, если | 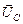 | < |
| < | 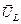 | (рис. 16.32, а), либо отставать на p/2, если |
| (рис. 16.32, а), либо отставать на p/2, если | 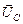 | > |
| > | 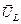 | (рис. 16.32, б).
| (рис. 16.32, б).
В общем случае
U0 = |UC – UL| = |I0XC – I0XL| = I0 |XC – XL| = 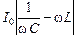 ,
,
отсюда
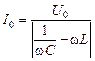 . (16.34)
. (16.34)
Величину
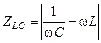 (16.35)
(16.35)
назовем полным сопротивлением LC-цепи. Тогда можно записать
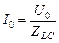 . (16.36)
. (16.36)
Для амплитуд UC и UL справедливо
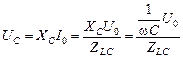 . (16.37)
. (16.37)
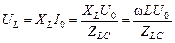 . (16.38)
. (16.38)
Сдвиг по фазе между напряжением и током равен:
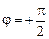 (ток опережает напряжение), если ХС > XL;
(ток опережает напряжение), если ХС > XL;
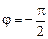 (ток отстает от напряжения), если ХС < XL.
(ток отстает от напряжения), если ХС < XL.
Соответственно, функция i(t) имеет вид
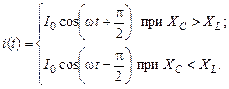 (16.39)
(16.39)
Задача 16.9. Найти полное сопротивление цепи, состоящей из последовательно включенных конденсатора емкостью С = 0,10 мкФ и катушки с индуктивностью L = 0,50 Гн, при частоте тока n = = 1,0 кГц. При какой частоте n0 полное сопротивление цепи равно нулю?
| С = 0,10 мкФ = = 1,0×10–7 Ф L = 0,50 Гн n = 1,0 кГц | Решение. Полное сопротивление найдем по формуле (16.35):
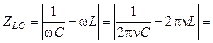
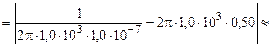
| |
| n0 = ? | ||
» 1,6×103 Ом = 1,6 кОм.
Если ZLC = 0, то
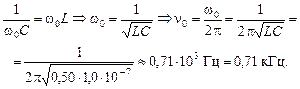
Ответ: 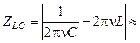 1,6 кОм;
1,6 кОм; 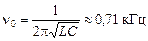 .
.
СТОП! Решите самостоятельно: В28, В29, С10, С11.
RLC-цепь
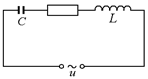 Рис. 16.33
Рис. 16.33
|
Рассмотрим цепь переменного тока, состоящую из последовательно соединенных конденсатора емкостью С, резистора сопротивлением R и катушки с индуктивностью L (рис. 16.33).
Пусть переменное напряжение в сети изменяется по закону u(t) = U0coswt.
Попробуем найти: 1) амплитуду тока I0; 2) амплитуду напряжения на конденсаторе UС; 3) амплитуду напряжения на катушке UL; 4) амплитуду напряжения на резисторе UR; 5) сдвиг фаз j между током и общим напряжением; 6) функцию i(t).
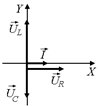 Рис. 16.34
Рис. 16.34
|
Изобразим на векторной диаграмме (рис. 16.34) векторы 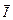 ,
, 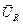 ,
, 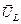 ,
, 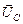 , как мы уже делали в предыдущих случаях, с учетом сдвига фаз между колебаниями:
, как мы уже делали в предыдущих случаях, с учетом сдвига фаз между колебаниями: 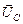 отстает от
отстает от 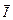 на p/2,
на p/2, 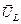 опережает
опережает 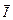 на p/2,
на p/2, 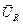 имеет одну фазу с
имеет одну фазу с 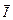 .
.
Введем вектор 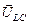 =
= 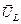 +
+ 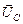 . Если UL > UC, то вектор
. Если UL > UC, то вектор 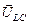 направлен вверх (рис. 16.35, а), а если UL < UC, то вектор
направлен вверх (рис. 16.35, а), а если UL < UC, то вектор 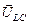 направлен вниз (рис. 16.35, б).
направлен вниз (рис. 16.35, б).
Рис. 16.35 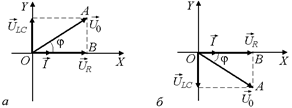
Амплитуду напряжения U0 находим из DАОВ на рис. 16.35, а и б:
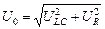 ,
,
где ULC = |UL – UC|. Тогда
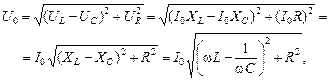
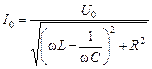 . (16.40)
. (16.40)
Величину
Z = 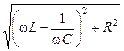 (16.41)
(16.41)
назовем импедансом. Тогда можно записать:
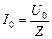 . (16.42)
. (16.42)
Для амплитуд напряжений UR, UL, UC справедливы формулы:
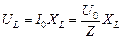 , (16.43)
, (16.43)
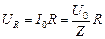 , (16.44)
, (16.44)
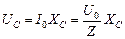 . (16.43)
. (16.43)
Сдвиг фаз между током и общим напряжением находим из DОАВ (cм. рис. 16.35):
tgj = 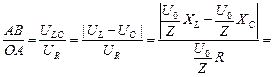
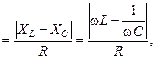
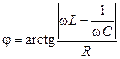 . (16.46)
. (16.46)
В случае XL > XC ток отстает от напряжения на j, поэтому если u(t) = U0coswt, тогда
i(t) = I0cos(wt – j).
В случае XL < XC ток опережает напряжение на j, поэтому если u(t) = U0coswt, тогда
i(t) = I0cos(wt + j).
Задача 16.10. Электрическая цепь состоит из резистора сопротивлением 4 Ом, катушки с индуктивным сопротивлением 8 Ом и конденсатора с емкостным сопротивлением 5 Ом, соединенных между собой последовательно. К концам цепи приложено напряжение 120 В. Найти силу тока в цепи и напряжение на всех участках, а также сдвиг фаз между током и напряжением. Все значения точные.
| R = 4 Ом XL = 8 Ом XC = 5 Ом Uд = 120 В | Решение. Заметим, что поскольку Uд = 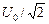 и Iд = и Iд = 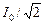 , то из формул (16.42)–(16.45) легко получить аналогичные формулы для действующих значений тока и напряжений: , то из формул (16.42)–(16.45) легко получить аналогичные формулы для действующих значений тока и напряжений:
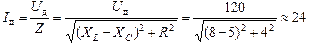 А. А.
|
| Iд = ? URд = ? ULд = ? UCд = ? j = ? |
URд = IдR = 24 А × 4 Ом = 96 В,
ULд = IдХL = 24 А × 8 Ом = 192 В,
UCд = IдХС = 24 А × 5 Ом = 120 В,
tgj = 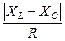 =
= 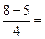 0,75, j = arctg
0,75, j = arctg 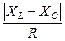 » 37°.
» 37°.
Поскольку XL > XC, то ток отстает от напряжения по фазе на j » 37°.
Ответ: Iд = 24 А; URд = 96 В; ULд = 192 В; UCд = 120 В; j » 37°.
СТОП! Решите самостоятельно: А14, А15, В31–В33, С12–С14.
Дата добавления: 2016-04-11; просмотров: 3994;
