Емкостное сопротивление

Рассмотрим экспериментальные факты.

1. Включим в цепь постоянного тока последовательно электрическую лампу и конденсатор (рис. 16.8, а). Лампа не горит, ведь конденсатор – это по сути дела разрыв цепи.

Рис. 16.8

2. Теперь включим те же лампу и конденсатор в цепь переменного тока (рис. 16.8, б). Лампа горит!

Читатель: Получается, что переменный ток проходит через конденсатор? А как же разрыв цепи?

Автор: Ток, конечно же, через конденсатор не проходит. Но происходит быстрая зарядка и разрядка конденсатора. А когда конденсатор заряжается и разряжается, через лампу идет ток (рис. 16.8, в).

3. Если мы «закоротим» конденсатор, т.е. пустим ток в обход (рис. 16.8, г), то лампа будет гореть ярче.

Читатель: Получается, что конденсатор как бы оказывает сопротивление переменному току?

Автор: Совершенно верно. И это сопротивление зависит от емкости конденсатора и частоты переменного тока. Экспериментально установлено, что если в схеме на рис. 16.8, б увеличить емкость конденсатора, то лампочка будет гореть ярче. Если при фиксированной емкости увеличивать частоту тока n, то лампочка также будет гореть ярче.

Читатель: Это вообще-то понятно. Чем больше емкость, тем дольше будет заряжаться конденсатор и тем меньше его поле будет «мешать» току зарядки. А чем больше частота тока, тем меньше будет заряд на конденсаторе и, опять же, тем меньше этот заряд будет «мешать» току.

Автор: Совершенно верно.

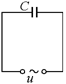Рис. 16.9

Рассмотрим цепь, состоящую только из источника переменного напряжения, которое меняется по закону и = U₀sinwt, и конденсатора с емкостью С (рис. 16.9). Найдем функцию зависимости тока от времени. Сначала выясним, чему равен заряд конденсатора в произвольный момент времени t.

Читатель: По-моему, на пластинах конденсатора в любой момент времени находятся равные по величине и противоположные по знаку заряды q и –q. Поэтому надо уточнить: заряд какой пластины мы рассматриваем?

Автор: Вы правы! Иначе наш ответ будет неопределенным с точностью до знака.

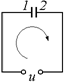Рис. 16.10

Введем направление обхода контура, т.е. ток, текущий в данном направлении, будем считать положительным, а в противоположном – отрицательным (рис. 16.10). И договоримся называть зарядом конденсатора заряд пластины 1, которая первой встретится при обходе контура. Тогда можно записать, что изменение заряда Dq равно произведению тока i(t) на время Dt:

Dq = i(t)Dt.

Переходя к бесконечно малым величинам, получим

.

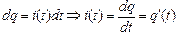С другой стороны, q(t) = Cu(t), тогда q(t) = CU₀sinwt, а

i(t) = q¢(t) = (CU₀sinwt)¢ = CU₀coswt×w = CwU₀coswt.

Итак, запомним:

i(t) = CwU₀coswt. (16.7)

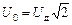Тогда амплитудное значение тока I₀ = CwU₀. С учетом того, что и , можно записать:

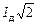= Þ .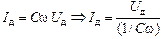

Величину 1/Сw называют емкостным сопротивлением:

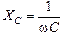. (16.8)

Тогда для действующих значений тока и напряжения выполняется закон Ома:

. (16.9)

Поскольку 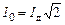и 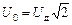, то для амплитудных значений тока и напряжения также справедливо

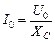. (16.9а)

Заметим, что если w ® 0, то Х_С ® ¥, т.е. если ток постоянный, то емкостное сопротивление бесконечно – через конденсатор в цепи постоянного тока ток не течет. Если С ® 0, то Х_С ® ¥, т.е. конденсатор бесконечно малой емкости – это просто разомкнутая цепь.

Построим графики зависимости тока и напряжения от времени (рис. 16.11): u(t) = U₀sinwt и i(t) = CwU₀coswt.

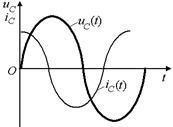Рис. 16.11

Из рисунка видно, что колебания силы тока опережают по фазе колебания напряжения на p/2. Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигнет максимума, сила тока становится равной нулю и т.д.

Заметим, что для мгновенных значений тока и напряжения в данном случае закон Ома не применим. В самом деле, в момент t = 0 i_C(0) = I₀, а и_С(0) = 0 (см. рис. 16.11). Это противоречит закону Ома.

СТОП! Решите самостоятельно: А7, В15.

Задача 16.5. К зажимам генератора присоединили конденсатор емкостью С = 0,1 мкФ. Найти амплитуду напряжения на зажимах, если амплитуда тока I₀ = 2,2 А, а период тока Т = 0,2 мс.

С = 0,1 мкФ = 1×10–7 Ф I0 = 2,2 А Т = 0,2 мс = 2×10–4 с	Решение. Воспользуемся формулами (16.8) и (16.9а). Получим
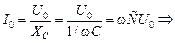
U0 = ?

.

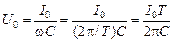Подставим численные значения:

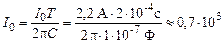В = 0,7 кВ.

Ответ: 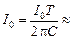0,7 кВ.

СТОП! Решите самостоятельно: А8, В16, В17.