Вращение рамки в однородном магнитном поле
Пусть прямоугольная рамка площадью S вращается в однородном магнитном поле с индукцией 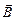 по часовой стрелке с угловой скоростью w. В начальный момент нормаль к рамке совпадет по направлению с вектором магнитной индукции
по часовой стрелке с угловой скоростью w. В начальный момент нормаль к рамке совпадет по направлению с вектором магнитной индукции 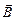 (рис. 11.22, а).
(рис. 11.22, а).
Рис. 11.22 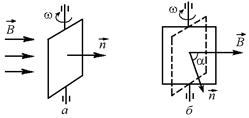
За время t рамка повернется на угол a = wt (рис. 11.22, б). Тогда поток магнитной индукции через рамку составит Ф = BScoswt. Вычислим ЭДС индукции по формуле (11.5):
ℰi = –Ф¢(t) = –( BScoswt)¢ = – BS(–sinwt)w = BSwsinwt.
Итак, запомним:
ℰi = BSwsinwt. (11.7)
Из формулы (11.7) следует, что:
1) ЭДС индукции изменяется по синусоидальному закону, т.е. вращение рамки с постоянной угловой скоростью в однородном магнитном поле порождает переменный ток;
2) амплитудное значение ЭДС ℰ0 = BSw;
3) максимального значения ЭДС индукции достигается при a = = 90° (когда 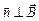 ), а минимального – при a = 0 и a = 180° (когда
), а минимального – при a = 0 и a = 180° (когда 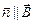 ).
).
СТОП! Решите самостоятельно: В19, С15–С17.
Читатель: А если вращать в магнитном поле не рамку, а катушку. имеющую N витков, ЭДС увеличится в N раз?
Автор: Совершенно верно. В этом случае будет справедлива формула
ℰi = NBSwsinwt. (11.8)
СТОП! Решите самостоятельно: В20–В23.
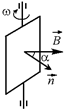 Рис. 11.23
Рис. 11.23
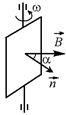 Рис. 11.24
Рис. 11.24
| Читатель: Мы рассмотрели случай, когда в начальный момент времени векторы 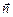 и и 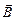 сонаправлены. А если они в момент t = 0 составляют некоторый угол a0 (рис. 11.23)?
Автор: В этом случае угол a(t) между векторами сонаправлены. А если они в момент t = 0 составляют некоторый угол a0 (рис. 11.23)?
Автор: В этом случае угол a(t) между векторами 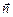 и и 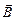 в момент времени t будет равен a(t) = a0 + wt, тогда Ф(t) = BSwсos(a0 + wt) и
ℰi = – Ф¢(t) = BSwsin(a0 + wt). (11.9)
Читатель: А если рамка будет вращаться против часовой стрелки (рис. 11.24)?
Автор: В этом случае угол a будет убывать:
a(t) = a0 – wt,
Ф(t) = BSwcos(a0 – wt),
ℰi = – Ф¢(t) = –BSwsin(a0 – wt). (11.10) в момент времени t будет равен a(t) = a0 + wt, тогда Ф(t) = BSwсos(a0 + wt) и
ℰi = – Ф¢(t) = BSwsin(a0 + wt). (11.9)
Читатель: А если рамка будет вращаться против часовой стрелки (рис. 11.24)?
Автор: В этом случае угол a будет убывать:
a(t) = a0 – wt,
Ф(t) = BSwcos(a0 – wt),
ℰi = – Ф¢(t) = –BSwsin(a0 – wt). (11.10)
|
Заметим, что если a0 = 0, то ℰi, вычисленные по формулам (11.9) и (11.10), будут иметь одинаковые значение:
ℰ 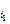 = BSwsinwt = ℰ
= BSwsinwt = ℰ 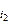 = –BSwsin(0 – wt) = +BSwsinwt,
= –BSwsin(0 – wt) = +BSwsinwt,
т.е. если рамка начинает вращаться из положения, когда 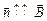 , то независимо от направления вращения справедлива формула (11.7).
, то независимо от направления вращения справедлива формула (11.7).
СТОП! Решите самостоятельно: В24–В26, С16, С17, D2.
Дата добавления: 2016-04-11; просмотров: 7400;
