В однородном магнитном поле?
1. Если в начальный момент частица была неподвижна (υ = 0), то двигаться она вообще не будет, так как величина силы Лоренца FЛ = qυВsina также равна нулю. Траектория частицы – точка.
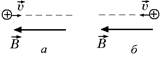 Рис. 9.23
Рис. 9.23
|
2. Если частица влетела в магнитное поле параллельно направлению поля (рис. 9.23, а и б), то магнитное поле никак не будет действовать на частицу, так как угол a между вектором скорости 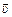 и вектором магнитной индукции
и вектором магнитной индукции 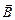 равен либо 0, либо 180°, sina = 0, FЛ = 0. Значит, частица сохранит свою скорость, а ее траектория – это прямая.
равен либо 0, либо 180°, sina = 0, FЛ = 0. Значит, частица сохранит свою скорость, а ее траектория – это прямая.
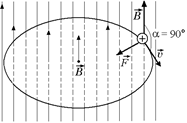 Рис. 9.24
Рис. 9.24
|
3. Пусть частица с зарядом q влетает в однородное магнитное поле с индукцией 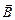 со скоростью υ, перпендикулярной к направлению поля (рис. 9.24). Так как магнитное поле не меняет модуля скорости, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что радиус кривизны R плоской траектории частицы постоянен. Частица равномерно движется по окружности радиусом R. Определим этот радиус. Согласно второму закону Ньютона
со скоростью υ, перпендикулярной к направлению поля (рис. 9.24). Так как магнитное поле не меняет модуля скорости, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что радиус кривизны R плоской траектории частицы постоянен. Частица равномерно движется по окружности радиусом R. Определим этот радиус. Согласно второму закону Ньютона
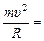 qυB.
qυB.
Отсюда
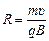 . (9.5)
. (9.5)
4. Рассмотрим самый трудный случай. Пусть положительно заряженная частица (например, a-частица, состоящая из двух протонов и двух нейтронов) начинает двигаться в однородном магнитном поле так, что вектор скорости 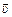 составляет с вектором магнитной индукции
составляет с вектором магнитной индукции 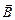 угол a. В этом случае вектор скорости
угол a. В этом случае вектор скорости 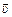 a-частицы можно представить как сумму двух векторов, из которых
a-частицы можно представить как сумму двух векторов, из которых 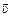 1 ^
1 ^ 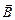 , a
, a 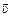 2||
2|| 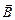 (рис. 9.25). Вектор
(рис. 9.25). Вектор 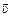 2 не меняется ни по модулю, ни по направлению, так как сила Лоренца не действует на частицу, имеющую скорость вдоль поля (вдоль вектора
2 не меняется ни по модулю, ни по направлению, так как сила Лоренца не действует на частицу, имеющую скорость вдоль поля (вдоль вектора 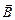 ). Вектор
). Вектор 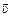 1меняется по направлению, так как на a-частицу действует сила Лоренца, постоянная по модулю и перпендикулярная скорости
1меняется по направлению, так как на a-частицу действует сила Лоренца, постоянная по модулю и перпендикулярная скорости 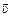 1. Эта сила сообщает a-частице постоянное по модулю ускорение, тоже перпендикулярное вектору
1. Эта сила сообщает a-частице постоянное по модулю ускорение, тоже перпендикулярное вектору 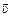 1.Но движение с постоянной по модулю скоростью и ускорением, перпендикулярным этой скорости, есть равномерное движение по окружности.
1.Но движение с постоянной по модулю скоростью и ускорением, перпендикулярным этой скорости, есть равномерное движение по окружности.
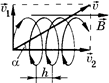 Рис. 9.25
Рис. 9.25
|
Таким образом, на равномерное движение вдоль линии индукции накладывается движение по окружности в плоскости, перпендикулярной вектору 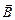 . А этозначит, что частица движется по винтовой линии с шагом h = υ2t, где t – время одного оборота a-частицы по окружности, радиус которой, согласно формуле (9.5), равен:
. А этозначит, что частица движется по винтовой линии с шагом h = υ2t, где t – время одного оборота a-частицы по окружности, радиус которой, согласно формуле (9.5), равен:
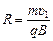 .
.
СТОП! Решите самостоятельно: А8, А9, В13–В18, С10, С11.
Масс-спектрограф
Выразим из формулы (9.5) величину q/m – удельный заряд частицы:
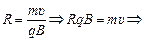
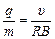 . (9.6)
. (9.6)
Если «заставить» заряженную частицу двигаться в магнитном поле с индукцией В по окружности радиуса R со скоростью υ, то по формуле (9.6) можно определить удельный заряд частицы.
С помощью магнитного поля можно разделять заряженные частицы по их удельным зарядам. Одновременно можно точно определять массы частиц. Разделение частиц осуществляется в приборах, называемых масс-спектрографами.
На рис. 9.26 изображена принципиальная схема простейшего масс-спектрографа. Вакуумная камера прибора помещена в магнитное поле (вектор индукции  перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с большой точностью измерить радиус траектории R. По этому радиусу определяется удельный заряд иона. Зная же заряд иона, легко определить его массу.
перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с большой точностью измерить радиус траектории R. По этому радиусу определяется удельный заряд иона. Зная же заряд иона, легко определить его массу.
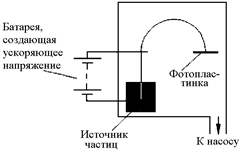 Рис. 9.26
Рис. 9.26
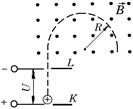 Рис. 9.27
Рис. 9.27
|
Задача 9.3.В масс-спектрографе (рис. 9.27) заряженные частицы ускоряются на участке KL электрическим полем и, попав в магнитное поле с индукцией  , описывают окружность радиусом R. Вывести формулу для расчета удельного заряда частицы q/m, если ускоряющее напряжение равно U,а начальную скорость частицы считать равной нулю.
, описывают окружность радиусом R. Вывести формулу для расчета удельного заряда частицы q/m, если ускоряющее напряжение равно U,а начальную скорость частицы считать равной нулю.
| B R U | Решение. На участке KL электрическое поле совершает над заряженной частицей работу А = qU, которая идет на увеличение ее кинетической энергии:
А = qU = 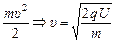 . (1) . (1)
|
| q/m = ? |
В магнитном поле частица движется по окружности, радиус которой определяется формулой (9.5):
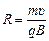 . (2)
. (2)
Подставляя (1) в (2), получим:
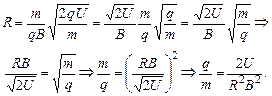
Ответ: 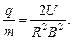
СТОП! Решите самостоятельно: А10, В19–В21, С12.
Дата добавления: 2016-04-11; просмотров: 2040;
