Вращение проводника в магнитном поле

Читатель: А если мы будем не перемещать проводник поступательно, а вращать в магнитном поле, то возникнет ли на его концах разность потенциалов (рис. 9.18)?

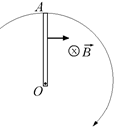Рис. 9.18 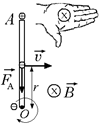Рис. 9.19

Автор: Обязательно возникнет! Рассмотрим электрон, находящийся на расстоянии r от центра вращения (рис. 9.19). На него будет действовать сила Лоренца, направление которой определяется правилом правой руки – к точке О. Значит, в центре будет «минус», а на краю стержня в точке А – «плюс».

Пусть стержень вращается с угловой скоростью ω, а его длина равна l, и пусть индукция магнитного поля равна В. Вычислим разность потенциалов U на концах стержня. Электрон, находящийся в точке С на расстоянии r от центра, движется по окружности радиуса r со скоростью υ = ωr, тогда величина силы Лоренца, действующая на него, равна F_Л = еυВ = еωrВ.

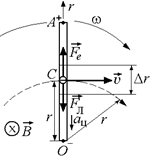Рис. 9.20

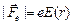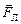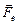Пусть напряженность электрического поля в данной точке равна Е(r), тогда на электрон действует «электрическая» сила , направленная от центра (рис. 9.20). Равнодействующая сил и сообщает электрону центростремительное ускорение а_ц = ω²r. Тогда согласно второму закону Ньютона имеем:

F_Л – F_e = mω²r Þ

еωrВ – eE(r) = mω²r. (1)

Здесь сделаем одно упрощающее предположение. Поскольку масса электрона т = 9,1×10^–31 кг очень мала по сравнению с его зарядом е = 1,6×10^–19 Кл, то будем считать, что mω²r » 0. Тогда

еωrВ – eE(r) = 0 Þ E(r) = ωrВ,

т.е. напряженность электрического поля в стержне линейно зависит от r. Следовательно, на малом промежутке Dr около точки С (см. рис. 9.20) разность потенциалов

DU = E(r)×Dr = ωBrDr.

Чтобы найти разность потенциалов на участке ОА, надо разбить длину ОА на малые участки Dr_i и вычислить сумму напряжений на этих участках:

.

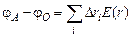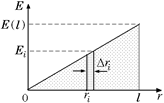Рис. 9.21

Это суммирование проще всего выполнить с помощью графика Е(r) (рис. 9.21). Ясно, что искомое напряжение равно площади под графиком на участке от 0 до l:

.

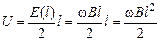Для тех, кто знаком с интегрированием, этот же результат можно получить еще проще:

.

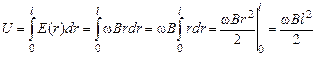Итак, запомним:

U = 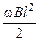. (9.4)

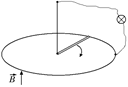Рис. 9.22

Читатель: А можно ли с помощью вращающегося стержня получить электрический ток?

Автор: Да, например, с помощью схемы на рис. 9.22.

СТОП! Решите самостоятельно: В12, С8, С9.