Движение электрона в однородном магнитном поле
Для решения этой задачи так же воспользуемся прямоугольной системой координат. Ось у направим навстречу вектору магнитной индукции В, а ось x – так, чтобы вектор скорости электрона u, находящегося в момент времени t = 0 в точке начала координат, лежал в плоскости XOY, т.е. имеем компоненты uxo и uyo.
В отсутствии электрического поля система уравнений движения электрона принимает вид:
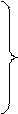 m
m 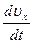 = – е ( uу × Вz – uz By );
= – е ( uу × Вz – uz By );
 m
m 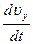 = – e (uz Bx – ux Bz );
= – e (uz Bx – ux Bz );
m 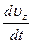 =– –e (ux By – uy Bx ),
=– –e (ux By – uy Bx ),
или с учетом условий Bx =Bz =0, а Ву = – В:
 m
m 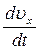 = e B uz;
= e B uz;
m 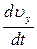 = 0;
= 0;
m 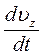 =e Bux.
=e Bux.

Рисунок 2.4. Движение электрона в однородном магнитном поле
Интегрирование второго уравнения системы с учетом начального условия: при t=0, uy=uyo приводит к соотношению:
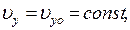
т.е. показывает, что магнитное поле не влияет на компоненту скорости электрона в направлении силовых линий поля.
Совместное решение первого и третьего уравнений системы, состоящее в дифференцировании первого по времени и подстановке значения duz /dt из третьего, приводит к уравнению, связывающему скорость электрона ux cо временем:
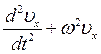 = 0,
= 0,
где 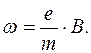
Решение уравнений такого типа можно представить в виде:
ux = A cosw t + C sinw t,
причем из начальных условий при t = 0, ux = uxo , dux /dt = 0 (что следует из первого уравнения системы, так как uzo = 0) вытекает, что
ux = uxo × cos w t.
Кроме того, дифференцирование этого уравнения с учетом первого уравнения системы приводит к выражению:
uz =uxo× sinw t.
Заметим, что возведение в квадрат и сложение двух последних уравнений дает выражение:
ux2 + uz2= uxo2 = const,
которое еще раз подтверждает, что магнитное поле не изменяет величины полной скорости (энергии) электрона.
В результате интегрирования уравнения, определяющего его ux, получаем:
x = 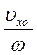 × sin w t,
× sin w t,
постоянная интегрирования в соответствии с начальными условиями равна нулю.
Интегрирование уравнения, определяющего скорость uz с учетом того, что при z = 0, t = 0 позволяет найти зависимость от времени координаты Z электрона:
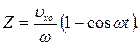
Решая два последних уравнения относительно sinwt и coswt, возводя в квадрат и складывая, после несложных преобразований получаем уравнение проекции траектории электрона на плоскости XOZ:
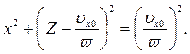
Это уравнение окружности радиуса r = 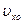 / w , центр которой расположен на оси z на расстоянии r от начала координат (рис. 2.4). Сама траектория электрона представляет собой цилиндрическую спираль радиуса
/ w , центр которой расположен на оси z на расстоянии r от начала координат (рис. 2.4). Сама траектория электрона представляет собой цилиндрическую спираль радиуса
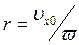
c шагом
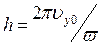 .
.
Из полученных уравнений очевидно также, что величина
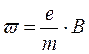
представляет собой круговую частоту движения электрона по этой траектории.
Дата добавления: 2016-03-15; просмотров: 1713;
