Скорость центра масс системы

Пусть имеется система точечных масс: т₁, т₂, …, т_п. Их положение в пространстве определяется радиусами-векторами 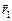, , …, 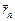. Тогда

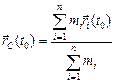. (1)

Пусть материальные точки движутся произвольным образом. Тогда через малое время Dt ® 0 их радиусы-векторы будут равны 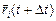, а для радиуса-вектора центра масс будет справедливо

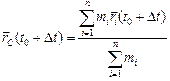. (2)

Вычтем (1) из (2) и разделим на Dt, получим

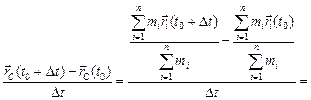
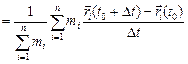. (3)

Поскольку – скорость центра масс, а 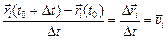– скорость i-й массы, то из равенства (3) получаем = .

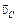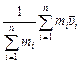Но 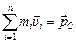– импульс системы, значит, 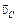= 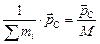, где 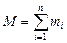– общая масса системы. Если система замкнута, то 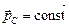, следовательно, 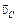= 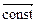, т.е. центр масс замкнутой системы движется с постоянной скоростью, равной импульсу системы, деленному на ее массу.

Задача 19.5. Лодка стоит неподвижно в стоячей воде. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние сдвинется лодка, если масса человека т = 60 кг, масса лодки М = 120 кг, длина лодки l = 3,0 м?

т = 60 кг М = 120 кг l = 3,0 м	а)	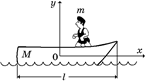б)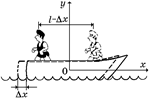
Dх = ?

Рис. 19.10

Решение. В начальный момент все тела неподвижны, поэтому скорость центра масс υ_С = 0 (рис. 19.10,а). А так как система человек–лодка замкнутая, то центр масс будет и дальше оставаться неподвижным: х_С = const.

Возьмем с.о. х0у с началом координат в центре масс системы (рис. 19.10,б). Пусть человек перешел с носа на корму. Если лодка сдвинулась вправо на Dх, то человек – влево на (l – Dх). Изменение координаты центра масс при этом равно нулю:

Dх_С = МDх + т(l – Dх) = 0 Þ Dх(т + М) = ml Þ

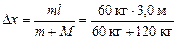= 1,0 м.

Ответ: 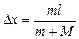= 1,0 м.

СТОП! Решите самостоятельно: С12–С15.