Задачи средней трудности. В1.К потолку лифта, движущегося с ускорением , направленным вверх, подвешен груз массы т на двух нитях
 В1.К потолку лифта, движущегося с ускорением
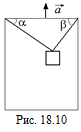
В1.К потолку лифта, движущегося с ускорением  , направленным вверх, подвешен груз массы т на двух нитях, составляющих углы a и b с горизонтальным потолком (рис. 18.10). Определить силы Т1 и Т2 натяжения левой и правой нитей.
, направленным вверх, подвешен груз массы т на двух нитях, составляющих углы a и b с горизонтальным потолком (рис. 18.10). Определить силы Т1 и Т2 натяжения левой и правой нитей.
В2.Шарик, подвешенный на нити, имеющей длину l, описывает окружность в горизонтальной плоскости, нить составляет с вертикалью угол a. Найти период t обращения шарика, если маятник находится в лифте, движущемся с постоянным ускорением а < g, направленным вниз.
В3.Легкая тележка может скатываться без трения с наклонной плоскости. На тележке укреплен отвес (шарик массы т на нитке) (рис. 18.11). Какое направление будет иметь нить отвеса при свободном скатывании тележки? До начала скатывания нить удерживалась в направлении, перпендикулярном к наклонной плоскости.
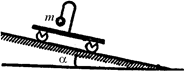 Рис. 18.11
Рис. 18.11
В4.На горизонтальной доске лежит груз. Коэффициент трения между доской и грузом k = 0,1. Какое ускорение а в горизонтальном направлении следует сообщить доске, чтобы груз мог с нее соскользнуть?
В5.На горизонтальной доске лежит кубик. Доске сообщают ускорение один раз 3 м/с2, а другой раз 0,5 м/с2 в горизонтальном направлении. С каким ускорением будет двигаться кубик относительно земли и относительно доски? Коэффициент трения между кубиком и доской 0,1, принять g = 10 м/с2.
В6.На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень с подвешенным на нити шариком массы т = 2 г. Найти силу натяжения Т нити, если плоскость образует с горизонтом угол a = 600.
В7.На гладкой наклонной плоскости, движущейся вправо с ускорением а, лежит брусок (рис. 18.12). Каким должно быть это ускорение, чтобы брусок не скользил по плоскости?
Рис. 18.12 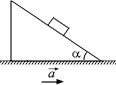 Рис. 18.13
Рис. 18.13 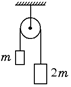
В8.Через невесомый блок перекинута веревка с грузами m и 2т (рис. 18.13). Блок движется вверх с ускорением b. Пренебрегая трением, найти давление блока на ось.
В9.Решить предыдущую задачу в предположении, что блок движется вниз с ускорением b < g.
В10.К потолку лифта, поднимающегося с ускорением а = 1,2 м/с2, направленным вверх, прикреплен динамометр. К динамометру подвешен блок, свободно вращающийся вокруг горизонтальной оси. Через блок перекинута нить, к концам которой прикреплены грузы массами т1 = 20 г и т2 = 300 г. Определите показания динамометра. Массой нити и блока пренебречь.
 В11.Небольшой грузик массы m = 20 г привязан тонкой нерастяжимой нитью к грани бруска массы М = 80 г, находящегося на гладкой горизонтальной поверхности. Если на брусок действовать горизонтальной силой, не превосходящей некоторого значения F0, то грузик скользит по горизонтальной поверхности, а нить образует с нею угол a = 31,6° (рис. 18.14);
В11.Небольшой грузик массы m = 20 г привязан тонкой нерастяжимой нитью к грани бруска массы М = 80 г, находящегося на гладкой горизонтальной поверхности. Если на брусок действовать горизонтальной силой, не превосходящей некоторого значения F0, то грузик скользит по горизонтальной поверхности, а нить образует с нею угол a = 31,6° (рис. 18.14);
а) определить силу F0, по достижении которой грузик начнет отставать от горизонтальной поверхности;
б) определить натяжение нити Т, когда на брусок действуют горизонтальной силой F0/2;
в) найти угол d, образуемый нитью Н с горизонтальной поверхностью, когда на брусок действуют горизонтальной силой 2F0.
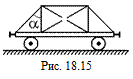 В12.Контейнер массы m = 3,0 т (рис. 18.15), установленный на гладкой горизонтальной платформе, закреплен с помощью натянутых тросов, образующих угол a = 60° с платформой. Когда платформа движется с ускорением а = 50 см/с2 по прямолинейной горизонтальной колее, натяжение одного троса исчезает, а натяжение другого увеличивается на h = 50 % по сравнению с тем, когда платформа движется без ускорения. Определить силу натяжения тросов Т на неподвижной платформе.
В12.Контейнер массы m = 3,0 т (рис. 18.15), установленный на гладкой горизонтальной платформе, закреплен с помощью натянутых тросов, образующих угол a = 60° с платформой. Когда платформа движется с ускорением а = 50 см/с2 по прямолинейной горизонтальной колее, натяжение одного троса исчезает, а натяжение другого увеличивается на h = 50 % по сравнению с тем, когда платформа движется без ускорения. Определить силу натяжения тросов Т на неподвижной платформе.
Задачи трудные
С1.На доске, движущейся в горизонтальном направлении с ускорением а0, находится плоская шайба, коэффициент трения которой о доску равен k. Построить график зависимости ускорения шайбы а от ускорения доски а0.
С2.Тонкая нерастяжимая нить, которой брусок привязан к призме, параллельна гладкой ее грани, где находится брусок (рис. 18.16). Брусок начинает скользить, когда призма движется с горизонтальным ускорением а1 = 2,10 м/с2, перпендикулярным к ребрам призмы. С каким минимальным горизонтальным ускорением а2 должна двигаться призма, чтобы брусок отстал от ее грани?
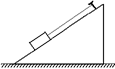
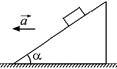
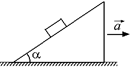
Рис. 18.16 Рис. 18.17 Рис. 18.18
С3.Наклонная плоскость с углом наклона a движется с ускорением а в сторону, указанную стрелкой (рис. 18.17). Начиная с какого значения а тело, лежащее на наклонной плоскости, начнет подниматься? Коэффициент трения между телом и наклонной плоскостью равен k.
С4. На наклонной плоскости с углом наклона a неподвижно лежит кубик, причем коэффициент трения между кубиком и плоскостью равен k. Наклонная плоскость движется с ускорением а в направлении, указанном стрелкой (рис. 18.18). При каком минимальном значении этого ускорения кубик начнет соскальзывать?
С5.На наклонной плоскости, образующей угол a с горизонтом, стоит кубик массы т. Плоскость находится в лифте, движущемся с ускорением а, направленным вверх. Найти силу нормального давления Fн.д кубика на плоскость. При каком коэффициенте трения k между кубиком и плоскостью кубик не будет соскальзывать вниз?
С6. На внутренней шероховатой поверхности сферы радиуса R = 60 см находится тело малых размеров. На какой максимальной высоте h от нижней точки сферы может удержаться это тело за счет трения, если вся система поднимается вертикально вверх с ускорением а = 2,5 м/с2. Коэффициент трения m = 0,30.
С7. К потолку лифта, движущегося с ускорением а = 2,00 м/с2, подвешен блок (рис. 18.19). Через блок перекинута нерастяжимая нить, к которой привязаны два груза массами т1 = 6,00 кг и т2 = 4,00 кг. Определить ускорения тел относительно блока и земли 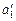 и и 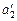 , а1 и а2. Считать массу блока и нити равными нулю.
С8. К потолку вагона, движущегося в горизонтальном направлении с ускорением а0 = 5,7 м/с2, прикреплен блок, через который перекинута нить с грузами т1 = 1,5 кг и т2 = 2,0 кг (рис. 18.20). Определите натяжение нити Т, а также модули ускорений , а1 и а2. Считать массу блока и нити равными нулю.
С8. К потолку вагона, движущегося в горизонтальном направлении с ускорением а0 = 5,7 м/с2, прикреплен блок, через который перекинута нить с грузами т1 = 1,5 кг и т2 = 2,0 кг (рис. 18.20). Определите натяжение нити Т, а также модули ускорений 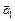 и и 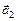 обоих грузов относительно Земли. Какой угол b с вертикалью образуют, указанные векторы? Нить нерастяжима, массой блока и нити пренебречь.
С9. Дана система грузов (рис. 18.21). Известно, что т1 = 2т, т2 = 3т, т3 = т. Вычислить ускорения грузов а и силы натяжения Т нитей.
С10.Посмотрите на рис. 18.22. Какую постоянную горизонтальную силу нужно приложить к М, чтобы М1 и М2 относительно М не двигались? Трения нет.
С11.На столе лежит деревянный брусок массы 2 кг, к которому привязана нить, перекинутая через блок, укрепленный на краю стола. К свободному обоих грузов относительно Земли. Какой угол b с вертикалью образуют, указанные векторы? Нить нерастяжима, массой блока и нити пренебречь.
С9. Дана система грузов (рис. 18.21). Известно, что т1 = 2т, т2 = 3т, т3 = т. Вычислить ускорения грузов а и силы натяжения Т нитей.
С10.Посмотрите на рис. 18.22. Какую постоянную горизонтальную силу нужно приложить к М, чтобы М1 и М2 относительно М не двигались? Трения нет.
С11.На столе лежит деревянный брусок массы 2 кг, к которому привязана нить, перекинутая через блок, укрепленный на краю стола. К свободному
| 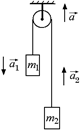 Рис. 18.19
Рис. 18.19
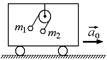 Рис. 18.20
Рис. 18.20
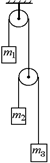 Рис. 18.21
Рис. 18.21
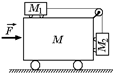 Рис. 18.22
Рис. 18.22
| |
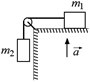 Рис. 18.23
Рис. 18.23
 Рис. 18.24
Рис. 18.24
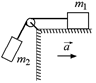 Рис. 18.25
Рис. 18.25
| концу нити подвешен груз 1,0 кг, вследствие чего брусок движется с ускорением 0,60 м/с2. Каково будет ускорение груза и бруска, если вся система будет: а) подниматься с ускорением 2,2 м/с2; б) опускаться с тем же ускорением?
С12.Система из двух грузов массами т1 и т2 (рис. 18.23) находится в лифте, движущемся с ускорением а, направленным вверх. Найти силу натяжения Т нити, если коэффициент трения между грузом и опорой равен k. Изменится ли состояние движения (или покоя) грузов, если ускорение лифта сменится на обратное?
С13.Вертикальная стенка движется горизонтально с ускорением а0. В контакте со стенкой находится брусок (рис. 18.24). Коэффициент трения между стенкой и бруском k = 0,40. Построить график зависимости силы трения fтp между бруском и стенкой от ускорения стенки а0. Определить модуль и направление вектора ускорения бруска 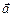 при: а) а0 = 30 м/с2; б) а0 = 10 м/с2. при: а) а0 = 30 м/с2; б) а0 = 10 м/с2.
| |
С14.Груз массы т1 находится на столе, который движется горизонтально с ускорением а (рис. 18.25). К грузу привязана нить, перекинутая через невесомый блок. К другому концу нити подвешен второй груз массы т2. Найти силу натяжения нити, если коэффициент трения груза т1 о стол равен m.
Дата добавления: 2016-04-11; просмотров: 4328;
