На закон сохранения импульса
1. Определить тела, входящие в систему.
2. Определить начальное и конечное состояния системы, сделать рисунок и указать на нем импульсы тел в конечном и начальном состояниях.
3. Установить, является ли система замкнутой. Если система не замкнута, то надо выбрать направление х, вдоль которого не действуют внешние силы или их векторная сумма равна нулю.
Если такого направления нет, то надо проанализировать, нельзя ли воспользоваться условием Dt ® 0, т.е. предположить, что действие внешних сил кратковременно.
4. Записать закон сохранения импульса или закон сохранения проекции импульса.
5. Решить полученные уравнения относительно неизвестных величин.
Задача 19.1. Граната, летящая со скоростью υ = 15 м/с, разорвалась на два осколка массами т1 = 6 кг и т2 = 14 кг. Скорость большего осколка возросла до υ2 = 24 м/с по направлению движения. Найти скорость и направление движения меньшего осколка.
| υ = 15 м/с υ2 = 24 м/с т1 = 6 кг т2 = 14 кг |  Рис. 19.3
Рис. 19.3
| Решение. Система состоит из двух тел т1 и т2, которые сначала движутся как единое целое. Начальное состояние – до разрыва гранаты, конечное – сразу после разрыва. |
| υ1 = ? | ||
На систему действует внешняя сила – сила тяжести, поэтому система незамкнутая. Проведем ось х в направлении движения гранаты (рис. 19.3) и учтем, что сила тяжести 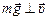 . Тогда так как проекция силы тяжести на эту ось равна нулю, воспользуемся законом сохранения проекции импульса:
. Тогда так как проекция силы тяжести на эту ось равна нулю, воспользуемся законом сохранения проекции импульса:
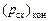 –
– 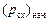 = 0.
= 0.
Учитывая, что 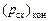 =
= 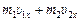 , а
, а 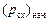 =
= 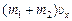 , получим
, получим 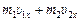 =
= 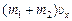 , откуда
, откуда
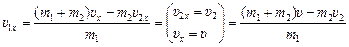 =
=
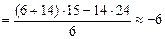 м/с.
м/с.
Так как υ1х< 0, то осколок т1 полетит в направлении, противоположном направлению движения гранаты.
Ответ: 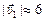 м/с,
м/с, 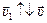 .
.
СТОП! Решите самостоятельно: А1, А2, С1, С2.
Задача 19.2.Два пластилиновых шарика массами m1 = 10 г и т2 = 20 г движутся по гладкому столу по взаимно перпендикулярным направлениям со скоростями υ1 = 3,0 м/с и υ2 = 2,0 м/c и абсолютно неупруго соударяются. Определить скорость шариков после соударения.
| m1 = 10 г m2 = 20 г υ1 = 3,0 м/с υ2 = 2,0 м/c | Решение. Система двух тел замкнута (внешних сил нет), поэтому
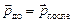 ; ;
 , ,
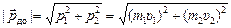 (рис. 19.4);
(рис. 19.4);
|  Рис. 19.4
Рис. 19.4
|
| υ = ? |
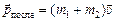 ;
;
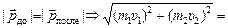
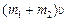 .
.
Отсюда находим ответ:  1,7 м/с.
1,7 м/с.
СТОП! Решите самостоятельно: В4, В5, С4, С5.
Задача 19.3. Мальчик массой т переходит с носа лодки на ее корму (рис. 19.5). Масса лодки М. С какой скоростью и будет перемещаться лодка, если скорость человека относительно лодки равна υ?
| т, М, υ | Рис. 19.5 
|
| и = ? | |
Решение. В начальный момент импульс системы человек–лодка был равен нулю. Так как в горизонтальном направлении на систему внешние силы не действуют: 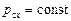 = 0.
= 0.
 Пусть ось х совпадает с направлением движения лодки (рис. 19.6). Тогда скорость человека относительно воды будет равна υ¢ = υ – и. Отсюда
Пусть ось х совпадает с направлением движения лодки (рис. 19.6). Тогда скорость человека относительно воды будет равна υ¢ = υ – и. Отсюда
рсх = Ми – тυ¢ = Ми – т(υ – и) = 0 Þ(М + т)и = тυ Þ
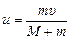 .
.
Ответ: 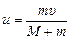 .
.
СТОП! Решите самостоятельно: В7, С7, С8.
Центр инерции (центр масс)
Пусть имеются п точечных масс: т1, т2, …, тп. Их положение в пространстве задается в некоторой с.о. с помощью радиусов-векторов 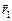 ,
,  , …,
, …, 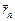 (рис. 19.7). Тогда точка С, определяемая радиусом-вектором
(рис. 19.7). Тогда точка С, определяемая радиусом-вектором

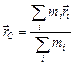 , (19.7)
, (19.7)
называется центром инерции или центром масс системы. Соответственно координаты хС и уС точки С задаются выражениями
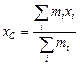 ,
, 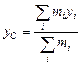 , (19.8)
, (19.8)
где хi и уi – проекции радиуса-вектора  на оси х и у.
на оси х и у.
Задача 19.4. Масса Земли в 81 раз больше массы Луны. Расстояние между центрами Земли и Луны равно 60 земным радиусам. Где находится центр инерции системы Земля–Луна?
| RЗ = 6400 км МЛ = МЗ/81 RЛ =60RЗ | Решение. Пусть хЗ = 0, хЛ = 60RЗ (рис. 19.8).
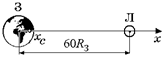 Рис. 19.8 Рис. 19.8
|
| хС = ? | |
Тогда согласно формуле (19.8)
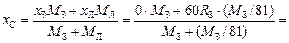
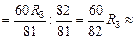 0,74RЗ » 0,74×6400 км » 4,7×103 км.
0,74RЗ » 0,74×6400 км » 4,7×103 км.
Ответ: центр инерции находится внутри земного шара на прямой, соединяющей центры Земли и Луны на расстоянии хС » » 4,7×103 км от центра Земли.
Дата добавления: 2016-04-11; просмотров: 1838;
