ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ

Механическим движением называется изменение положения тела относительно других тел с течением времени.

Если это положение с течением времени не меняется, значит, тело относительно других тел (тела) не движется. Например, если два автомобиля едут по шоссе друг за другом так, что расстояние между ними с течением вре­мени не меняется, значит, они покоятся относительно друг друга.

А если дерево, растущее у дороги, удаляется относи­тельно проехавшего мимо мотоциклиста, значит, дерево движется относительно мотоциклиста.

Траекториейназывается линия, вдоль которой дви­жется тело.

Например, линия, прочерченная мелом на доске, – это траектория кусочка мела; светящийся след, оставленный в ночном небе метеоритом, – это траектория метеорита; ломаная линия, по которой движется молеку­ла газа, – это траектория молекулы газа.

Путь – это расстояние, пройденное телом, отсчиты­ваемое вдоль траектории.

Путь – величина неотрицательная и измеряется в единицах длины: километрах (км), метрах (м), сантимет­рах (см), миллиметрах (мм) и т.д.

Кинематика – это часть механики, которая изучает движение тел без исследования причин, вызывающих это движение. Такой подход по­зволяет выявить особенности различных видов движения и рассмотреть их физические характеристики. Однако более полное понимание движе­ния возможно только при анализе взаимодействия движущегося тела с другими телами, что является предметом динамики.

Движение происходит как в пространстве, так и во времени. Опи­сать движение тела означает указать для каждого момента времени по­ложение тела в пространстве и его скорость. Основная задача кинема­тики заключается втом, чтобы, зная положение тела в некоторый мо­мент времени, а также законы движения, определить его положение в любой последующий момент времени.

Система отсчета. Для описания движения изучаемого тела (ма­териальной точки) необходимо выбрать другое тело, называемое телом отсчета, а чтобы отмечать моменты времени, требуются часы. Однако выбор тела отсчета еще не дает возможность полностью описать движе­ние материальной точки. Например, чтобы знать положение ракеты в воздухе в любой момент времени, недостаточно условиться рассматри­вать ее движение, положим, относительно Земли. Необходимо как-то ма­тематически описать движение, т.е. задать величины, позволяющие од­нозначно определить движение ракеты. Для этого с телом отсчета свя­зывают систему координат. Таким образом, координатная система, свя­занная с каким-либо реальным телом (телом отсчета), а также часы для отсчета времени образуют систему отсчета, относительно которой и рас­сматривается движение материальной точки.

Следует отчетливо понимать различие между телом отсчета и си­стемой координат. Тело отсчета образуют реальные тела, в то время как система координат является математической абстракцией. Обычно выбор системы координат определяется соображениями удобства. Мы зна­комы с декартовой прямоугольной системой координат. С ней мы будем работать и в дальнейшем. Но существует полярные, сферические и другие системы координат, удобные для рассмотрения определенного класса задач.

Способы описания движения.В механике используют три спо­соба аналитического описания движения материальной точки в простран­стве (мы ограничимся движением точки на плоскости).

Первый способ – векторный. Он основан на том, что положение материальной точки А в момент времени t определяется радиусом-векто­ром 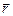, идущим из начала координат к движущейся точке А (рис. 1.1,а). Кривая, которую при движении описывает точка А и, следовательно, конец радиуса-вектора 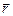, называется траекторией. Понятно, что траектория имеет различный вид в разных системах координат.

Второй способ описания – координатный. Положение точки на плоскости в момент времени t₁определяется заданием двух координат х₁ и у₁ (рис. 1.1,б). При движении точки А ее координаты изменяются во времени: х = х(t) и у = у(t). Если эти функции известны, то они определяют положение точки на плоскости в любой момент времени. Зависимость х(t) называют законом движения точки по оси 0х, y(t) – законом движения по оси 0у.

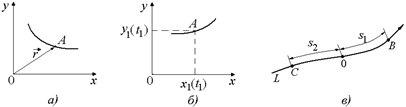
Рис. 1.1

Легко видеть, что между векторным и координатным способом существует простая связь. Как известно, любой вектор можно задать его проекциями на оси координат. В нашем случае проекции радиуса-вектора 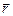совпадают с координатами точки. Если заданы функции x(t)и y(t), то, очевидно, известно положение радиуса-вектора 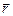= 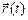. Функцию 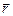= 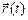называют векторным законом движения точки.

Третий способ описания получил название "естественного" или "траекторного". Этот способ применяют тогда, когда траектория точки известна заранее. Пусть задана линия L, по которой происходит движение (рис. 1.1,в). Укажем на этой линии точку начала отсчета (или нулевую) – точку 0 и зададим стрелкой положительное направление. Тогда противоположное направление будет считаться отрицательным.

Линию l с выбранным положительным направлением и точкой начала отсчета будем называть координатной осью. Положение точки на линии L будем задавать числом, которое будем называть координатой точки.

Координата точкина координатной оси равна расстоянию от начала координат до данной точки, отсчитанному вдоль координатной оси и взятому со знаком «плюс», если точка удалена от начала координат в положительном направлении, и со знаком «минус», если точка удалена от начала координат в отрицательном направлении. Например, координата точки В на рис. 1.1,в равна +s₁: х_В = +s₁,координата точки С равна –s₂: x_С = –s₂.

Если известна зависимость координаты точки от времени х(t), то мы знаем положение точки в любой момент времени.