ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПУТИ НА ГРАФИКЕ
ЗАВИСИМОСТИ υ = υ(t)
Мгновенной путевой скоростью называется величина, равная отношению 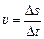 при
при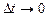 ,где Ds – приращение пути, пройденного телом за время Dt.
,где Ds – приращение пути, пройденного телом за время Dt.
 Секущая к графику s(t), проходящая через точки М (t1;s1) и N (t2;s2) представляет собой график равномерного движения (рис. 3.1), скорость которого равна средней путевой скорости на интервале времени [t1; t2]. Чем круче идет секущая MN, т.е. чем больший угол a она составляет с осью t, тем бóльшую среднюю скорость имеет тело на участке [t1; t2].
Секущая к графику s(t), проходящая через точки М (t1;s1) и N (t2;s2) представляет собой график равномерного движения (рис. 3.1), скорость которого равна средней путевой скорости на интервале времени [t1; t2]. Чем круче идет секущая MN, т.е. чем больший угол a она составляет с осью t, тем бóльшую среднюю скорость имеет тело на участке [t1; t2].
Если устремить Dt к нулю, секущая превратится в касательную к графику s(t).
Чем больше угол наклона касательной к графику s(t), тем больше мгновенная путевая скорость в данный момент.
СТОП! Решите самостоятельно: А1, А2, В1–В3.
Геометрический смысл пути на графике υ = υ(t)
Задача 3.1.Дан график зависимости υ = υ(t) = const (рис. 3.2). Найти путь за промежуток времени [t1; t2].
 Решение. Так как движение равномерное, то s = υ0Dt = υ0(t2 – t1). С другой стороны, υ0 – это высота, а (t2 – t1) – основание прямоугольника ABCD под графиком υ = υ(t) (рис. 3.2). Поэтому получается, что путь можно вычислить так, как если бы мы определяли площадь прямоугольника ABCD со сторонами υ0 и (t2 – t1).
Решение. Так как движение равномерное, то s = υ0Dt = υ0(t2 – t1). С другой стороны, υ0 – это высота, а (t2 – t1) – основание прямоугольника ABCD под графиком υ = υ(t) (рис. 3.2). Поэтому получается, что путь можно вычислить так, как если бы мы определяли площадь прямоугольника ABCD со сторонами υ0 и (t2 – t1).
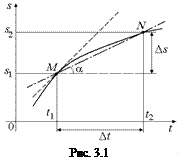
Задача 3.2. По графику υ(t) (рис. 3.3) определить путь, пройденный за промежуток времени [t1; t2]. Величины Dt1, Dt2, Dt3, Dt4, υ1, υ2, υ3, υ4 заданы.
Решение. Так как на каждом из промежутков Dti движение равномерное, то путь равен:
s = υ1Dt1 + υ2Dt2 + υ3Dt3 + υ4Dt4 = 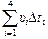 .
.
Заметим, что путь вычисляется как сумма площадей прямоугольников со сторонами υi и Dti, и это есть площадь под графиком υ(t) на участке [t1; t2].
Задача 3.3. По графику υ(t) (рис. 3.4) определить путь, пройденный за промежуток времени [0; t].
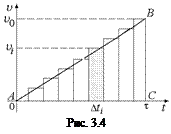 Решение. Разобьем интервал времени [0; t] на N малых интервалов Dti
Решение. Разобьем интервал времени [0; t] на N малых интервалов Dti 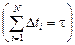 , таких, что в пределах каждого Dti значение υi можно считать практически постоянным. Тогда согласно задаче 3.2 путь можно вычислить как сумму площадей прямоугольников со сторонами Dti и υi. Но если N ® ¥, то сумма этих площадей будет стремиться к площади под графиком υ(t), т.е. к площади прямоугольного треугольника АВС с катетами υ0 и t:
, таких, что в пределах каждого Dti значение υi можно считать практически постоянным. Тогда согласно задаче 3.2 путь можно вычислить как сумму площадей прямоугольников со сторонами Dti и υi. Но если N ® ¥, то сумма этих площадей будет стремиться к площади под графиком υ(t), т.е. к площади прямоугольного треугольника АВС с катетами υ0 и t: 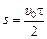 .
.
Вывод: путь можно вычислять как площадь под графиком υ(t).
СТОП! Решите самостоятельно: С3.
Читатель: По-моему, все-таки нельзя говорить, что путь равен площади под графиком. Это неверно хотя бы из соображений размерности: ведь путь измеряется в метрах, а площадь в квадратных сантиметрах!
Автор: Вы совершенно правы! Давайте разберемся: какая связь между площадью под графиком υ(t), выраженной в см2, и пройденным путем, выраженным в м.
Что такое масштаб?
Масштабом называется величина, равная отношению длины отрезка, изображающего на графике (карте, чертеже) физическую величину, к реальному значению этой величины:
| М = | Длина изображения величины |
| Реальное значение величины |
Пример 3.1. На географической карте отрезок 1 см изображает расстояние 1 км на местности. В этом случае масштаб равен
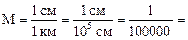 1 : 100 000.
1 : 100 000.
Пример 3.2. Отрезок 1 см изображает на графике промежуток времени t = 10 с. Тогда 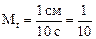 (см/с).
(см/с).
Пример 3.3. Отрезок 1 см изображает на графике скорость υ = = 2 м/с. Тогда 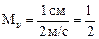 (см/(м/с)).
(см/(м/с)).
Пример 3.4. Пусть отрезок Dх изображает время Dt, а Мt – масштаб времени на графике. Тогда 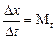 .
.
Пример 3.5. Пусть отрезок у изображает скорость υ, а Мυ – масштаб времени на графике. Тогда 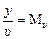 .
.
Задача 3.4. Дан произвольный график υ = υ(t) (рис. 3.5). Площадь под графиком на участке [t1; t2] известна и равна Sгр (см2). Масштаб скорости Мυ (см/(м/с)) и масштаб времени Мt (см/с) заданы. Определить путь, пройденный за промежуток времени [t1; t2].
| Sгр Мυ (см/(м/с)) Мt (см/с) | Решение. Разобьем отрезок [t1; t2] на малые интервалы Dti (i = 1, 2, … N; N ® ¥). Пусть υi – скорость, соответствующая интервалу Dti, тогда путь
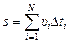 . (1) . (1)
| |
| s = ? | ||
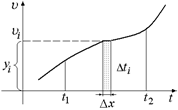 Рис. 3.5
Рис. 3.5
| Пусть Dхi – отрезок (см), изображающий время Dti, а уi – отрезок (см), изображающий скорость υi, тогда:
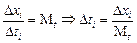 ; ;
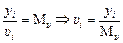 . .
| |
Подставляя эти выражения в (1), получаем
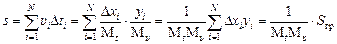
Ответ: 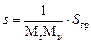 .
.
Итак, запомним, что путь равен:
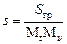 , (3.1)
, (3.1)
где sгр– площадь под графиком.
Задача 3.5. Дан график υ = υ(t), имеющий вид полуокружности с центром в точке [t; 0] (рис. 3.6). Найти путь за промежуток време-
| ни [0; 2t]. | Рис. 3.6 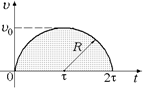
|
| υ0 t | |
| s = ? |
Решение. Пусть R – радиус окружности, [R] = см, Мt – масштаб времени, [Мt] = см/с; Мυ – масштаб скорости, [Мυ] = см/(м/с). Тогда согласно формуле (3.1) находим путь:
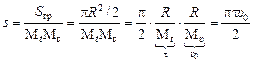 .
.
Ответ: 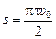 .
.
СТОП! Решите самостоятельно: С1, С2.
Дата добавления: 2016-04-11; просмотров: 2402;
