ДВИЖЕНИЕ ПО ЗАДАННОЙ ТРАЕКТОРИИ
Средней путевой скоростью называется физическая величина, равная отношению величины пройденного телом пути ко времени, в течение которого этот путь был пройден.
| СРЕДНЯЯ ПУТЕВАЯ СКОРОСТЬ = | ПРОЙДЕННЫЙ ПУТЬ |
| время прохождения пути |
Если обозначить путь буквой s, время – буквой t, a среднюю путевую скорость буквой υ,получим следующую формулу:
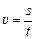 . (2.1)
. (2.1)
Задача 2.1. Два легкоатлета совершали разминку. Первый легкоатлет первую треть всего пути пробежал со скоростью υ1 = =10,0 км/ч, а остальную часть пути шел со скоростью υ2 = 5,0 км/ч. Второй легкоатлет первую треть всего времени разминки бежал со скоростью и1 = 10,0 км/ч, а остальное время шел со скоростью и2 = =5,0 км/ч. Определите среднюю путевую скорость каждого легкоатлета.
| υ1 = 10,0 км/ч, υ2 = 5,0 км/ч, и1 = 10,0 км/ч и2 = 5,0 км/ч | Решение.
1. Пусть s – весь путь первого легкоатлета, тогда время его движения
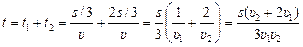 . .
|
| υср = ? иср = ? |
Отсюда 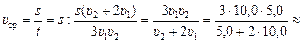 6,0 км/ч.
6,0 км/ч.
2. Пусть t – все время движения второго легкоатлета, тогда пройденный им путь
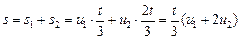 .
.
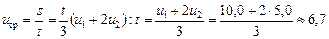 км/ч.
км/ч.
Ответ: υср = 6,0 км/ч; иср = 6,7 км/ч.
СТОП! Решите самостоятельно: А1, А2, В2, С1.
Движение называется равномерным, если за любые равные промежутки времени тело проходит одинаковые пути.
Путевой скоростью равномерного движенияназывается величина, равная отношению пути s ко времени t, за которое этот путь был пройден
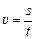 . (2.2)
. (2.2)
Если тело начало равномерное движение по заданной траектории из координаты х0 в момент времени t0 с путевой скоростью υ, то его координата х в момент времени t > t0 будет равна
х(t) = x0 + υ(t – t0), (2.3)
если движение происходит в положительном направлении, и
х(t) = x0 – υ(t – t0), (2.4)
если движение происходит в отрицательном направлении.
Задача 2.2. Из одного города в другой вышел пешеход. Когда он прошел путь s1 = 27 км, вслед ему выехал автомобиль со скоростью, в k раз большей, чем шел пешеход. Второго города они достигли одновременно. Каково расстояние sх между городами?
Разобрать случай, когда k = 10. Построить график s(t) для обоих тел.
| s1 = 27 км k = 10 | Решение. Запишем уравнения движения для пешехода и автомобиля: х1(t) = υ1t; x2(t) = υ2(t – t), |
| sх = ? |
где υ1 – скорость пешехода; υ2 – скорость автомобиля; t – момент отправления автомобиля. По условию задачи
s1 = υ1t. (1)
В момент прибытия в пункт назначения tв координаты пешехода и автомобиля равны
υ1tв = υ2(tв – t). (2)
Скорость автомобиля в k раз больше скорости пешехода:
υ2 = kυ1. (3)
Искомая величина sх равна
sx = υ1tв. (4)
Решим систему уравнений (1)–(4). Из (1) выделим 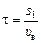 и подставим t и υ2 = kυ1 в (2), получим
и подставим t и υ2 = kυ1 в (2), получим
υ1tв = kυ1 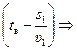 υ1tв(k – 1) = ks1.
υ1tв(k – 1) = ks1.
Заменим υ1tв из (4) на sx:
 км.
км.
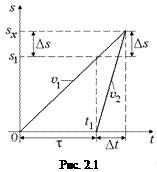 Заметим, что с помощью графика (рис. 2.1) задача решается значительно проще. Как видно из графика, за время Dt тела прошли пути:
Заметим, что с помощью графика (рис. 2.1) задача решается значительно проще. Как видно из графика, за время Dt тела прошли пути:
1-е тело:
Ds = υ1Dt Þ sx – s1 = υ1Dt; (1)
2-e тело:
sx = υ2Dt Þ sx = kυ1Dt; (2)
(1): (2) Þ 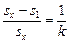 ;
; 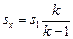 ;
;
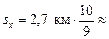 30 км.
30 км.
Ответ: 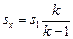 » 30 км.
» 30 км.
СТОП! Решите самостоятельно: С4, С5, С7.
В целом ряде задач на равномерное движение удобно записывать уравнение движения в системе отсчета, связанной с движущимися телами, например, водой в реке, эскалатором в метро, движущимся автомобилем и т.д.
Задача 2.3.Мимо пристани проходит плот. В этот момент в поселок, находящийся на расстоянии s1 = 15 км от пристани, вниз по реке отправляется моторная лодка. Она дошла до поселка за время t = 3/4 ч и, повернув обратно, встретила плот на расстоянии s2 = 9 км от поселка. Каковы скорость течения реки и скорость лодки относительно воды?
| s1 = 15 км s2 = 9 км t = 3/4 ч | Решение. Выберем в качестве системы отсчета плот (воду). В этой системе отсчета лодка движется вниз и вверх по реке с одинаковой скоростью. Это означает, что время удаления лодки от плота равно времени приближения к нему. Таким образом, лодка |
| и = ? υ = ? | |
возвращалась к плоту такое же время, какое она удалялась от него: 3/4 ч. За прошедшие 1,5 ч плот прошел расстояние s1 – s2 = 6 км. Следовательно, скорость течения (скорость плота относительно берега) и = 4 км/ч. Скорость лодки υ относительно воды найдем из уравнения υ + и = s1/t Þ υ = s1/t – и = 16 км/ч.
Ответ: и = 4 км/ч, υ = 16 км/ч.
Это решение иллюстрирует, насколько важен в кинематике удачный выбор системы отсчета.
СТОП! Решите самостоятельно: В5–В7, С9, С11, С12.
Дата добавления: 2016-04-11; просмотров: 1795;
