Эквипотенциальные поверхности
Задача 9.2.Определить, может ли электростатическое поле иметь картину силовых линий, изображенную на рис. 9.3.
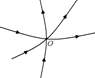
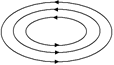
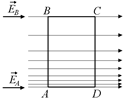
а б в
Рис. 9.3
Решение. В случае на рис. 9.3,а силовые линии пересекаются в одной точке, поэтому направление вектора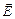 
в точке О не определено. Такое может быть только в том случае, если в точке О находится точечный заряд. Но если бы в точке О находился точечный заряд, то все линии либо входили в точку О (см. рис. 9.1,б), либо исходили из нее. В данном случае это не так, значит, такого поля не может быть.
В случае, показанном на рис. 9.3,б, при перемещении заряда вдоль силовой линии, поле будет совершать положительную работу по замкнутому контуру, следовательно, поле, изображенное на рис. 9.3,б, не является электростатическим.
Возьмем контур в виде прямоугольника ABCD (рис. 9.3,в). Рассмотрим работу поля по перемещению заряда +q по этому контуру:
;
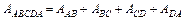ААВ = АCD = 0, так как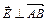 
, 
;
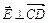ABC = EB×BC > 0;
ADA = EA×ADcos180° = –EA×AD < 0.
Учтем, что AD = ВС. Кроме того, поскольку силовые линии в нижней части рисунка «гуще», чем в верхней, то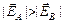 
. Отсюда
.
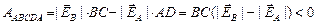Так как работа поля по замкнутому контуру не равна нулю, значит, изображенное на рис. 9.3,в поле не является электростатическим.
СТОП! Решите самостоятельно: А1, А3–А5, В2.
Поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью.
Задача 9.3. Доказать, что в каждой точке поля силовые линии перпендикулярны эквипотенциальной поверхности.
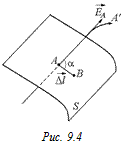Решение. Пусть через точку А проходит силовая линия АА¢ и эквипотенциальная поверхность S (рис. 9.4). Напряженность в точке А равна 
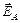. Переместим заряд q из точки А в точку В (В Î S). Перемещение 
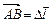будем считать настолько малым, что 
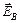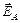= . Вычислим работу поля на участке 
:
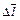1) AA®B = q(jA – jB) = 0 (jA = jB, так как потенциалы всех точек поверхности S равны);
2) 
.
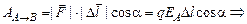
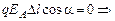
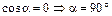Итак, a = 90°, то есть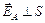 
, что и требовалось доказать.
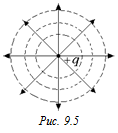Задача 9.4. Нарисовать картину эквипотенциальных поверхностей для поля точечного заряда +q.
Решение. Эквипотенциальные поверхности – это концентрические сферы с центром в заряде +q (рис. 9.5).
СТОП! Решите самостоятельно: А2, В5, В6.
Дата добавления: 2016-04-11; просмотров: 1217;