Задачи очень трудные. D1. Два длинных коаксиальных проводящих цилиндра заряжены так, что на далеком расстоянии от их концов на единицу длины внутреннего цилиндра приходится l1
D1. Два длинных коаксиальных проводящих цилиндра заряжены так, что на далеком расстоянии от их концов на единицу длины внутреннего цилиндра приходится l1 кулонов, а на единицу длины внешнего цилиндра l2 кулонов. Внутренний и внешний радиусы внутреннего цилиндра равны r1 и r2, а внешнего цилиндра равны r3 и r4. Найдите поле Е(r) в точках, расположенных вблизи середины цилиндров (т.е. там, где краевыми эффектами можно пренебречь). Определите разность потенциалов между цилиндрами.
Опишите качественно, в какую сторону будут меняться напряженность поля и потенциал, если: 1) r1 будет уменьшаться; 2) r2 будет уменьшаться; 3) внешний контур сечения внутреннего цилиндра имеет форму квадрата со сторонами, равными 2r2 (при этом предполагается, что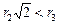 
)?
D2. Заряженная полусфера. Поверхность полусферической чаши радиуса R с тонкими стенками заряжена с постоянной плотностью. Определить потенциал в каждой точке поверхности, которая стянула бы чашу, как «кожа на барабане».
D3. Прямоугольный пластмассовый брусок с размерами 1 см ´ 10 см ´ ´100 см равномерно заряжен. Плотность зарядов равна r Кл/см3. Нарисуйте примерный ход потенциала j как функции расстояния до центра бруска вдоль прямой линии, перпендикулярной стенке с размерами 10 см ´ 100 см и проходящей через центр бруска. Рассмотрите интервал расстояний от 0,001 см (внутри бруска) до расстояний, во много раз превышающих 100 см. Масштаб возьмите дважды логарифмический, т.е. нарисуйте logj как функцию логарифма расстояния. На том же графике нарисуйте кривую зависимости напряженности электрического поля Е от расстояния.
СИЛОВЫЕ ЛИНИИ И ЭКВИПОТЕНЦИАЛЬНЫЕ
ПОВЕРХНОСТИ
Силовые линии
Читатель: Как нарисовать векторное поле на бумаге?
Автор: Это можно сделать двумя способами.
1. В каждой точке чертежа рисуется вектор, указывающий величину и направление векторного поля в данной точке.
2. Векторное поле изображают в виде непрерывных линий поля (в случае силового поля эти линии называются силовыми линиями), которые удовлетворяют следующим требованиям:
а) вектор поля в каждой точке направлен по касательной к линии поля, проходящей через данную точку;
б) линии поля имеют направление, совпадающее с направлением вектора поля в каждой точке;
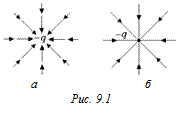в) густота линий поля (число линий, пересекающих единицу поверхности, расположенной перпендикулярно к направлению линий) пропорциональна модулю поля 
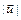в каждой точке.
Для примера на рис. 9.1 изображено поле вектора напряженности точечного заряда (–q) этими двумя способами.
Задача 9.1. Нарисовать картину силовых линий двух точечных зарядов: а) +q и –q; б)+10q и –q.
Решение. Выделим три характерные точки: А, Б и В и в них найдем направление вектора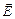 
с помощью векторного сложения. Учтем симметрию задачи относительно прямой, соединяющей заряды.
Ответ: рис. 9.2.
Заметим, что в случае б) заряд –q играет роль небольшого возмущения, вносимого в поле точечного заряда +10q. Большинство силовых линий (9/10), исходящих из заряда +10q, уходит на бесконечность и лишь 1/10 из них заканчивается на заряде –q.
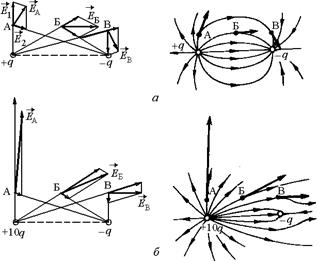
Рис. 9.2
СТОП! Решите самостоятельно: В4, С2.
Дата добавления: 2016-04-11; просмотров: 1233;