Потенциал поля равномерно

Связь между напряженностью

И потенциалом

Задача 8.1.Точки 1 и 2 лежат на оси 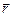(рис. 8.1). В точке 1 потенциал поля равен j₁, а в точке 2 – j₂. Расстояние между этими точками Dr настолько мало, что на всем этом участке напряженность поля можно считать постоянной величиной. Определить проекцию E_r вектора напряженности на ось 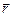. Известно, что .

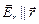j1 j2 Dr	Рис. 8.1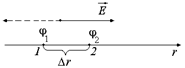
= ?

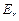Решение. Переместим пробный заряд q_пр > 0 из точки 1 в точку 2 и вычислим работу поля по его перемещению.С одной стороны:

А₁₂ = q_пр(j₁ – j₂).

С другой стороны:

А₁₂ = .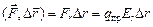

Отсюда

q_пр(j₁ – j₂) = 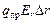Þ .

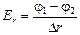Ответ:

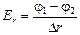. (8.1)

В СИ 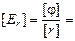В/м. Следовательно, [E] = В/м = Н/Кл.

Заметим, что:

если j₁ > j₂, то 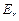> 0, ;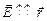

если j₁ < j₂, то 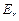< 0, .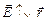

Читатель: Пусть j₁ > j₂. Поместим между точкой 1 и точкой 2 частицу: а) протон; б) электрон. Движение возможно только по оси 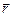. Куда будет двигаться частица?

Автор: В случае а) 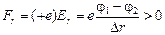Þ 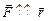, то есть протон будет двигаться вдоль оси 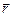. В случае б) 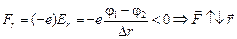, электрон будет двигаться в направлении, противоположном направлению оси .

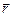Вывод: положительно заряженная частица всегда движется от точки с бóльшим потенциалом к точке с меньшим потенциалом, а отрицательно заряженная частица – наоборот.

Для тех, кто немного знаком с высшей математикой, отметим, что если в выражении (8.1) устремить Dr к нулю, то можно записать:

.

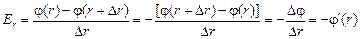То есть Е_r равен производной функции j по координате r, взятой со знаком «минус»:

Е_r 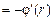. (8.2)

С помощью формулы (8.2) можно по известной функции j(r) найти функцию Е_r. Например, пусть j(r) = 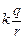– потенциал поля точечного заряда. Тогда 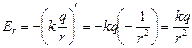– известная нам зависимость напряженности от расстояния до точечного заряда.

Пусть известна зависимость проекции вектора напряженности на ось 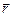: Е_r(r). Определим разность потенциалов между точками 1 и 2 с координатами r и r + Dr (см. рис. 8.1), считая, что Dr ® 0. Переместим заряд q_приз точки 1 в точку 2, тогда работа поля по перемещению будет равна:

с одной стороны, А₁₂ = q_пр(j(r) – j(r + Dr));

с другой стороны: А₁₂ = .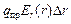

Отсюда

q_пр(j(r) – j(r + Dr)) = 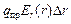Þ

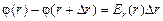. (8.3)

Величину 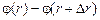еще называют убылью потенциала (убыль – это: [то, что было] – [то, что стало]).

Вывод: убыль потенциала от точки r до точки r + Dr равна произведению проекции вектора напряженности Е_r(r) на Dr.

Читатель: А как определить убыль потенциала j(r₁) – j(r₂), если величину r₂ – r₁ = Dr нельзя считать малой?

Автор: Рассмотрим график зависимости Е_r(r) для данного электрического поля (рис. 8.2,а). Видно, что j(r) – j(r + Dr) для малого участка Dr может быть вычислена как площадь прямоугольника со сторонами Е_r(r) и Dr. Тогда, разбивая отрезок [r₁; r₂] на малые участки Dr_i, получим, что убыль потенциала j(r₁) – j(r₂) может быть вычислена как площадь под графиком функции Е_r(r) на участке [r₁; r₂] (рис. 8.2,б).

а) 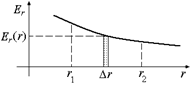б)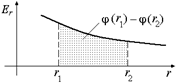

Рис. 8.2

Для тех, кто немного знаком с высшей математикой: площадь криволинейной трапеции (под графиком на рис. 8.2,б) в высшей математике вычисляется как определенный интеграл от функции Е_r(r) на участке [r₁; r₂]:

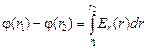. (8.4)

Задача 8.2. Две разноименно заряженные бесконечные пластины с поверхностной плотностью заряда s находятся на расстоянии d друг от друга. Определите разность потенциалов между пластинами.

s d	Решение. 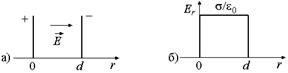Рис. 8.3
j+ – j– = ?

Способ 1. Напряженность поля между пластинами равна по модулю s/e₀ и направлена от плюса к минусу (рис. 8.3,а).

Площадь под графиком Е_r(r) на участке [0; d] равна (s/e₀)d. Убыль потенциала j(0) – j(d) = j⁺ – j^– как раз и равна этой площади:

j⁺ – j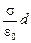^– = . (8.5)

Способ 2. Вычислим работу по перемещению пробного заряда q_пр с положительной пластины на отрицательную:

А = q_прЕd =q_пр(j⁺ – j^–).

Отсюда Еd = j⁺ – j^–, а так как 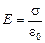, то

j⁺ – j^– = .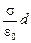

Заметим, что если электрическое поле однородное, т.е. 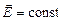, то для любого расстояния Dr можно записать

j₁ – j₂ = Е_rDr. (8.6)

Убыль потенциала j₁ – j₂ иногда называют электрическим напряжением.

СТОП! Решите самостоятельно: А1–А3, В1, В2, С1.

Задача 8.3. Между горизонтально расположенными разноименно заряженными плоскостями падает положительно заряженная пылинка массой т и зарядом q > 0. С каким ускорением движется пылинка, если разность потенциалов между пластинами j₁ – j₂ = Dj. Расстояние между пластинами равно d. Рассмотреть два случая (рис. 8.4).

q т d Dj	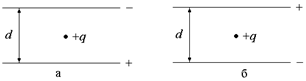Рис. 8.4
а = ?

Решение. В обоих случаях

.

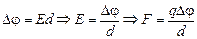В случае, показанном на рис. 8.5,а,

.

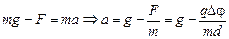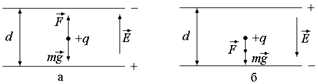
Рис. 8.5

В случае, показанном на рис. 8.5,б,

.

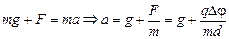Ответ: а) а 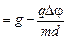; б) .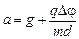

СТОП! Решите самостоятельно: А4, А5, В3, В5.

Потенциал поля равномерно

Заряженной сферы

Задача 8.4. Построить графики зависимости потенциала от расстояния до центра равномерно заряженной сферы зарядом Q и радиуса R.

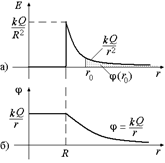		Рис. 8.6
Q R	Решение. График зависимости Е(r) для поля равномерно заряженной сферы мы уже строили в
j(r) = ?
§ 4. Будем строить график j(r) непосредственно под графиком Е(r) (рис. 8.6,а). Рассмотрим участок от R до ¥. На этом участке зависимость

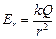точно такая же, как для поля точечного заряда Q, расположенного в центре сферы. Поэтому очевидно, что и зависимость j(r) на участке [R; +¥) будет такая же, как и для поля точечного заряда: 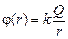. Ведь потенциал в произвольной точке r₀ > R j(r₀) – это площадь под графиком Е(r) на участке от r₀ до ¥ (см. рис. 8.6,а). А поскольку график Е(r) ничем не отличается на этом участке от графика Е(r) для поля точечного заряда, то и площадь под графиком Е(r) на участке [r₀; +¥) точно такая же, как и для точечного заряда (рис. 8.6,б). Следовательно, потенциал поля в произвольной точке r₀ > R равен

.

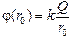Рассмотрим участок [0; R]. На этом участке Е = 0. Согласно формуле (8.6) для произвольной точки r₀, где r₀ Î [0; R), справедливо

j(r₀) – j(R) = 0×(R – r₀) = 0

или

.

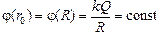То есть график j(r) на участке (0; R) – это отрезок прямой, параллельный оси r (см. рис. 8.6,б).

Ответ:

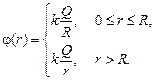(8.7)

СТОП! Решите самостоятельно: В8, В10, В15, С6, С7.

Задача 8.5. Электрическое поле создано двумя концентрическими равномерно заряженными сферами соответственно с зарядами Q₁ и Q₂ и радиусами R₁ и R₂ (R₁ < R₂). Построить график зависимости потенциала от расстояния до центра сфер.

Q1 Q2 R1 R2	Решение. Воспользуемся результатом задачи 8.4 – формулой (8.7). Запишем потенциалы полей, созданных каждой сферой в отдельности:
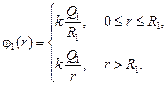
j(r) = ?

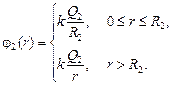
Как мы выяснили в § 6, потенциал поля, созданного совокупностью зарядов, равен сумме потенциалов полей, созданных каждым зарядом в отдельности. Поэтому искомый потенциал

j(r) = j₁(r) + j₂(r).

Пусть 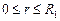, тогда .

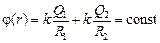Пусть 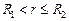, тогда .

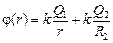Пусть 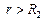, тогда .

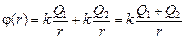График j(r) показан на рис. 8.7.

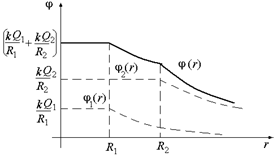
Рис. 8.7

Заметим, что если график Е(r) может иметь разрывы, то график j(r) всегда непрерывен. В самом деле, пусть график j(r) имеет разрыв в точке r₀ (рис. 8.8). Возьмем на оси r две точки А и В, такие, что АВ = Dr ® 0. Переместим заряд q­_пр из точки А в точку В. Тогда работа поля по перемещению заряда q­_пр будет равна

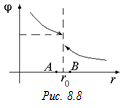А_АВ = q­_пр(j_А – j_В) = q­_прЕ(r₀)Dr.

Отсюда

,

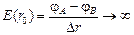так как Dr ® 0. То есть разрыв функции j(r) означает, что в этой точке напряженность поля стремится к бесконечности, что невозможно.

СТОП! Решите самостоятельно: С8, С9, С10.