Задачи средней трудности. В1. Найти напряжение между точками А и В (рис

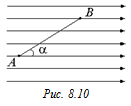
В1. Найти напряжение между точками А и В (рис. 8.10), если çАВç= 8,0 см, a = 30° и напряженность поля 50 кВ/м.

В2. Точка А лежит на линии напряженности однородного поля, напряженность которого 60 кВ/м. Найти разность потенциалов между точкой А и некоей точкой В, расположенной в 10 см от точки А. Рассмотреть случаи, когда точки А и В лежат: а) на одной линии напряженности; б) на прямой, перпендикулярной линии напряженности; в) на прямой, направленной под углом 45° к линиям напряженности.

В3. Капля масла диаметром 0,010 мм удерживается в равновесии между горизонтальными пластинами, расстояние между которыми равно 25 мм. Какой заряд находится на капле, если равновесие достигается, когда разность потенциалов между пластинами равна 3,6×10⁴ В? Плотность масла 0,80 г/см³.

В4. Пылинка массой 1,0×10^–11 г имеет заряд, равный 20 элементарным зарядам, и находится в равновесии между двумя горизонтальными параллельными пластинами с разностью потенциалов 153 В. Каково расстояние между пластинами? В каком направлении и с каким ускорением будет двигаться пылинка, если разность потенциалов на пластинах увеличить на 2,0 В?

В5. Между двумя пластинами, расположенными горизонтально в вакууме на расстоянии 4,8 мм друг от друга, находится в равновесии отрицательно заряженная капелька масла массой 10 нг. Сколько «избыточных» электронов имеет капелька, если на пластины подано напряжение 1,0 кВ?

После облучения капельки она стала двигаться вниз с ускорением 6,0 м/с². Сколько электронов потеряла капелька?

В6. На расстоянии а = 16 см от центра равномерно заряженной сферы радиуса R = 11 мм напряженность электрического поля Е = 77 Н/Кл. Определить потенциал j сферы и поверхностную плотность заряда s на сфере.

В7. Полый шар равномерно заряжен электричеством. Найти плотность его заряда как функцию радиуса и потенциала шара.

В8. Полый шар с центром О равномерно заряжен электричеством. В центре шара потенциал равен 100 В, а в точке А (ОА = 30 см) потенциал равен 50 В. Каков радиус шара?

В9. Определить потенциал находящегося в вакууме шара радиуса 10,0 см, если на расстоянии 1,00 м от его поверхности потенциал равен 20,0 В. Какой заряд сообщен шару? (Заряд равномерно распределен по поверхности шара.)

В10. На поверхности шара радиуса r₀ = 9,0 см равномерно распределен положительный заряд q = 0,10 нКл. Найти напряженность и потенциал в центре шара и на расстоянии r = 90 см от центра.

В11. Два шара – большой и маленький – равномерно заряжены электричеством с поверхностной плотностью s. Будут ли одинаковы потенциалы шаров?

В12. Две наэлектризованные пластины образовали однородное поле напряженностью 250 В/см. Каково напряжение на пластинах? С какой силой поле действует на заряд 6,0×10^–6 Кл и какую работу совершает, перемещая его от одной пластины к другой, если расстояние между ними 4,0 см?

В13. Две плоские одинаковые пластины находятся на расстоянии, малом по сравнению с их размерами. На одной из пластин находится заряд +q, на другой +4q. Определить разность потенциалов между пластинами. Площадь каждой пластины S, а расстояние между ними d.

В14. Между параллельными плоскими металлическими пластинами с зарядами +q и –q расстояние 2 см и разность потенциалов 300 В. Как изменится разность потенциалов, если пластины раздвинуть до 6 см?

В15. Какую работу А необходимо совершить, чтобы перенести заряд q = 3,0×10^–8 Кл из бесконечности в точку, находящуюся на расстоянии l = 90 см от поверхности сферы радиуса R = 10 см, если поверхностная плотность заряда сферы s = 2,0×10^–6 Кл/м²?

В16. Вектор электрического поля Е направлен вдоль оси 0х, и его проекция на эту ось зависит от координаты х так, как показано на рис. 8.11. Найти разность потенциалов между точками х₁ = – 1 см и х₂ = 6 см. Какая система заряженных тел могла бы быть источником такого поля?

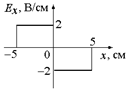Рис. 8.11 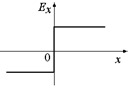Рис 8.12

В17. На рис. 8.12 приведен график зависимости Е_х(х) – проекции напряженности электрического поля на ось х от координаты х на этой оси. Построить график зависимости потенциала j(x) от координаты х. Считать j(0) = 0.

Задачи трудные

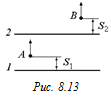С1. Бесконечные плоскости 1 и 2 параллельны друг другу и заряжены с одинаковой плотностью s (рис. 8.13). Зная расстояния точек А и В от плоскостей, найти разность потенциалов между этими точками.

С2. Решить задачу С1 в случае, когда точка А лежит под плоскостью 1.

С3. Чему равна разность потенциалов между крайними пластинами в системе, состоящей из трех параллельных пластин, заряженных одноименными зарядами с поверхностной плотностью заряда s₁, s₂, s₃? Средняя пластина находится на расстоянии h₁ от первой и на расстоянии h₂ от третьей пластины.

С4. Сфера радиуса R имеет заряд Q. Чему равен потенциал поля в центре сферы? Зависит ли потенциал поля на поверхности сферы от распределения заряда по сфере?

С5. На расстоянии 50 см от поверхности шара радиуса 9 см, заряженного до потенциала 25 кВ, находится точечный заряд 1,0×10^–8 Кл. Какую работу надо совершить для уменьшения расстояния между шаром и зарядом до 20 см?

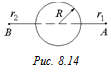
С6. Сфера радиуса R = 0,1 м заряжена до потенциала j = 300 В. Определить работу А сил электрического поля при перенесении заряда q = 1×10^–10 Кл из точки А в точку В (рис. 8.14), которые удалены от поверхности сферы на расстояния соответственно r₁ = 0,1 м, r₂ = =0,2 м. Влиянием заряда q на потенциал сферы пренебречь.

С7. Определить потенциал на поверхности заряженной сферы, если работа по перенесению заряда q = 2,0×10^–8 Кл из бесконечности в точку, находящуюся на расстоянии d = 1,0 см от поверхности сферы радиуса r = 1,0 см, равна А = 1,3×10^–5 Дж.

С8. Поле создано двумя равномерно заряженными концентрическими сферами. Найти потенциал в центре, а также в точках, отстоящих от центра на расстояниях r₁ = 20 см и r₂ = 50 см. Заряды сфер равны соответственно q₁ = 1,0 нКл и q₂ = –1,0 нКл, а их радиусы R₁ = 10 см и R₂ = 30 см.

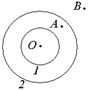Рис. 8.15

С9. Поле создано двумя равномерно заряженными концентрическими сферами (рис. 8.15). Найти потенциал точек О, А, В, зная, что заряды сфер равны Q1 и Q2, их радиусы равны R1 и R2, а расстояния ОА и ОВ равны l1 и l2. С10. Внутри тонкой сферы радиуса R находится сфера радиуса r. Сфере радиуса R сообщается заряд Q, а сфере радиуса r – заряд q. Определить потенциалы поверхности сфер.

С11. Две концентрические проводящие сферы радиусами R₁ и R₂ несут заряды +q и –q (рис. 8.16). Построить графики зависимости напряженности и потенциала электрического поля от расстояния до центра сфер и найти разность потенциалов сфер.

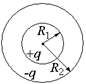Рис. 8.16 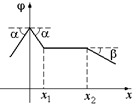Рис. 8.17

С12. Зависимость потенциала электростатического поля от координаты х представлена на рис. 8.17. Постройте график зависимости проекции напряженности электростатического поля Е_х от координаты х и изобразите систему тел, которые могли бы создать такое поле.

С13. На рис. 8.18 показан график зависимости напряженности поля, создаваемого двумя заряженными шарами, центры которых находятся в точках О₁ и О₂. Постройте график распределения потенциала между этими точками.

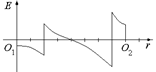Рис. 8.18 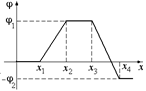Рис. 8.19

С14. На рис. 8.19 приведен график зависимости потенциала j от координаты х. Построить график зависимости от х проекции напряженности электрического поля Е_х(х).

С15. Построить графики изменения напряженности и потенциала поля вдоль линии, проходящей через два точечных заряда, находящихся на расстоянии 2d друг от друга. Величины зарядов равны: а) +q и –q; б) +q и +q; в) +q и –3q.

С16. Чему равна разность потенциалов между центром и поверхностью равномерно заряженного шара радиуса R, имеющего объемную плотность заряда r? Между осью и поверхностью равномерно заряженного бесконечного цилиндра радиуса R, имеющего объемную плотность заряда r? Между поверхностью равномерно заряженной пластины толщиной h, имеющей объемную плотность r, и серединой пластины?