Уравнение и передаточная функция системы автоматического регулирования

В общем виде замкнутая система автоматического регулирования состоит из объекта регулирования и регулятора (рис. 65).

Для получения уравнения системы необходимо задать свойства объекта регулирования (дифференциальное уравнение или передаточную функцию) и выбрать закон регулирования (П-, ПИ- или ПИД-законы, как наиболее часто используемые).

Пусть заданы уравнения объекта и регулятора. Получим уравнение системы в общем виде.

1. Объект регулирования (на примере одноемкостного статического объекта).

Уравнение объекта

.

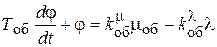В операторном виде

.

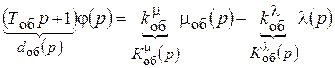Тогда уравнение объекта в операторном виде (общий вид для любого объекта) будет иметь вид

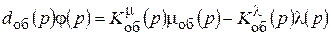(10.1)

d_об(р) – собственный оператор функции j; 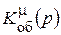, 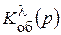- операторы воздействий по m_об и l.

2. Регулятор. Выберем ПИ-закон регулирования.

Уравнение ПИ-регулятора

.

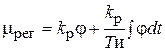Продифференцируем это уравнение по времени

.

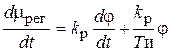Уравнение ПИ-закона в операторном виде

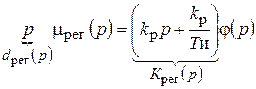. (10.2)

Тогда можно записать уравнение регулятора в операторном виде (общий вид для любого закона)

.

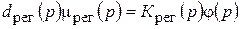d_рег(р) – собственный оператор функции m_рег; К_рег(р) - оператор воздействий по j.

Таким образом, используя общие уравнения объекта и регулятора в операторном виде (это алгебраическое уравнение), можно получить операторное уравнение системы регулирования в общем виде.

Имеем систему двух уравнений:

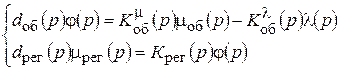
Регулятор является отрицательной обратной связью по отношению к объекту регулирования и воздействию на регулирующий орган (Р.О.).

Отсюда следует, что m_об= – m_рег. Тогда из уравнения регулятора имеем

.

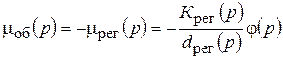Подставим это значение m_об в уравнение объекта, получаем

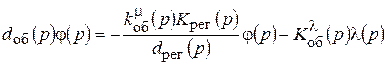
Или

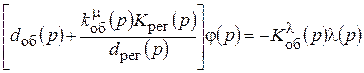(10.4)

Или

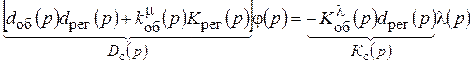(10.5)

где D_с(р) – собственный оператор функции; К_с(р) – оператор воздействий.

Тогда общий вид уравнения системы будет

.

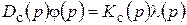Для получения дифференциального уравнения системы необходимо знать вид D_с(р) и К_с(р), которые зависят от типа объекта и выбранного закона регулирования.

Уравнение, записанное последним, называют уравнением вынужденного движения системы. Если правая часть этого уравнения равна нулю, то оно называется уравнением свободного движения системы:

D_с(р)j (р)=К_с(р)l (р) - уравнение вынужденного движения системы;

D_с(р)j=0 - уравнение свободного движения системы.

После того, как получено уравнение системы, оно исследуется на устойчивость и качество процесса регулирования. Из записи уравнения в общем виде следует

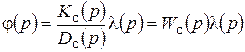, (10.6)

где 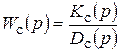- передаточная функция системы регулирования по возмущению l.

Рассмотрим, чему равна передаточная функция системы. Разделив все члены уравнения (10.3) на d_об(р), получим

.

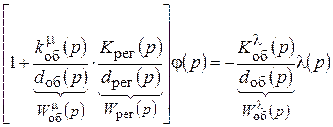Отношения 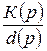представляют собой передаточные функции. Тогда уравнение системы можно записать через передаточные функции объекта и регулятора

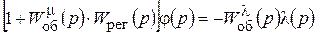(10.7)

Это записано операторное уравнение вынужденного движения системы через передаточные функции.

Уравнение свободного движения системы

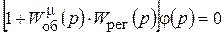(10.8)

Так как j в процессе регулирования все время изменяется и не равно 0, для того, чтобы уравнение свободного движения выполнялось, необходимо, чтобы выражение в квадратных скобках, равнялось нулю.

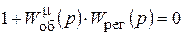(10.9)

Это уравнение называют характеристическим уравнением системы, записанным через передаточные функции. Оно используется для исследования устойчивости систем регулирования.

Рассмотрим конкретный пример получения уравнения системы регулирования:

1. Объект регулирования – одноемкостный статический

.

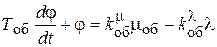2. ПИ-закон регулирования.

.

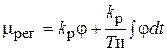Запишем эти уравнения в операторном виде

Объект: .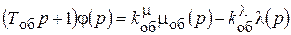

Регулятор: .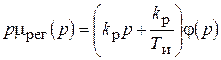

.

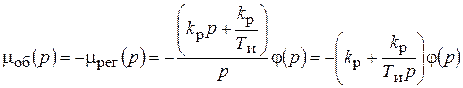Подставим это значение m_об в уравнение объекта регулирования, получим

,

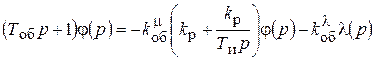Или

.

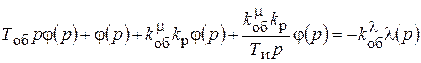Приведем к общему знаменателю и отбросим его

.

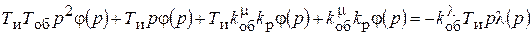Сгруппируем члены уравнения

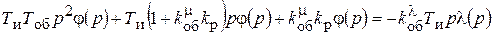
Это уравнение системы в операторном виде.

Запишем его, вынеся j за скобки

.

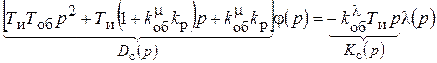Это уравнение вынужденного движения системы, в котором :

- собственный оператор функции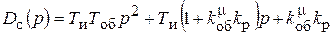

- оператор воздействий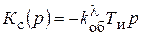

Уравнение свободного движения системы

.

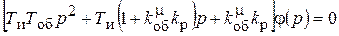Характеристическое уравнение системы

.

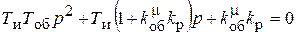Из уравнения системы видно, что его коэффициенты состоят из свойств объекта (Т_об, k_об^m, k_об^l) и параметров настроек регулятора (k_р, Т_и). Свойства объекта регулирования не изменяются, они характеризуют поведение объекта в статических и динамических режимах работы. Параметры настроек регуляторов (k_р, Т_и) можно изменять в широких пределах. Изменяя параметры настроек, добиваются, чтобы системы была устойчивой и отвечала необходимому качеству процесса регулирования.

Дифференциальное уравнение системы регулирования можно получить из операторного уравнения, заменяя оператор р на производные: ; .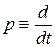

.

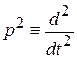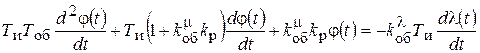Это дифференциальное уравнение вынужденного движения системы. Возмущение l - чаще всего однократное ступенчатое. Тогда l=const; 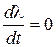, и после нанесения возмущения, правая часть уравнения равна нулю. Имеем уравнение свободного движения системы

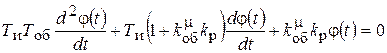
Оно исследуется на устойчивость. В него входят только коэффициенты усиления k_об^m, т.е. учитывается только воздействие по m_об.

Запись уравнения системы через передаточные функции.

Объект регулирования

.

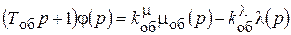Запишем его в виде

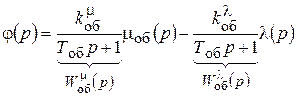; (10.10)

где 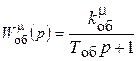; 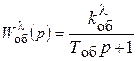- передаточные функции объекта по m_об и l.

Тогда уравнение (10.10) запишется в виде

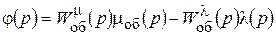. (10.11)

Регулятор

; ,

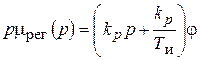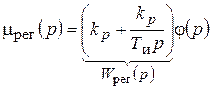где 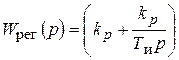- передаточная функция регулятора.

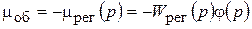. (10.12)

Подставив (10.12) в уравнение объекта (10.11), получим

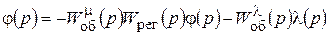(10.13)

Или

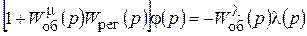(10.14)

Получили уравнение системы в операторном виде, записанное через передаточные функции объекта и регулятора.

Если в это уравнение подставить выражение передаточных функций объекта и регулятора, получим те же самые уравнения системы, выведенные ранее.