Понятие устойчивости систем регулирования
Система автоматического регулирования (САР) может быть устойчивой, неустойчивой и находится на границе устойчивости.
Система регулирования устойчива (то есть работоспособна), если регулируемый параметр j, после нанесения возмущения на объект, с течением времени устанавливается на новом значении или возвращается к заданному значению.
Система неустойчива, если регулируемый параметр j с течением времени неограниченно возрастает.
Система находится на границе устойчивости, если регулируемый параметр j не изменяется или совершает колебания с постоянной амплитудой.
Все виды устойчивости систем определяются решением уравнения свободного движения. Корни характеристического уравнения могут быть действительными числами, положительными или отрицательными, или комплексными числами с положительными, отрицательными или равными нулю действительными частями. Они и определяют устойчивость систем регулирования.
Рассмотрим это качественно на примере уравнения системы второго порядка.
Характеристическое уравнение рассмотренной ранее системы регулирования имеет вид
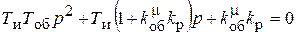
Перепишем его в удобном виде (как в инерционном элементе 2-го порядка)
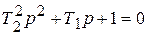 .
.
Здесь: 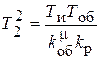 ;
; 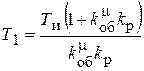 .
.
Уравнение имеет два корня р1 и р2.
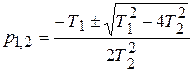 ,
,
или 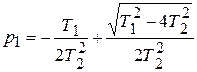 ;
; 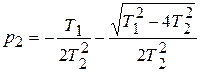 .
.
Рассмотрим различные случаи.
1. р1 и р2 – действительные числа.
Они получаются, если Т12-4Т22>0 в подкоренном выражении, т.е. Т1>2Т2. При этом соотношении коэффициентов получаем действительные корни. Они в общем случае могут быть положительными или отрицательными: р1,2>0; p1,2<0.
Дифференциальное уравнение свободного движения системы
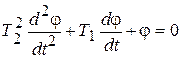 .
.
Его общее решение, как известно, представляет сумму экспонент
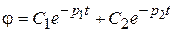
Тогда при p1,2<0, 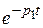 и
и 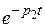 с течением времени t стремятся к нулю. Параметр jустанавливается на каком-то значении. Система устойчива (рис.66).
с течением времени t стремятся к нулю. Параметр jустанавливается на каком-то значении. Система устойчива (рис.66).
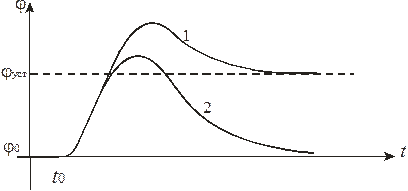
| Рис. 70. Процесс апериодический. Система устойчива. 1 – статическая система (П-закон); 2 – астатическая система (ПИ-, ПИД-законы). Процессы апериодические (неколебательные). Системы устойчивы. |
При p1,2>0 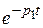 и
и 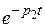 с течением времени неограниченно растут. Система неустойчива.
с течением времени неограниченно растут. Система неустойчива.
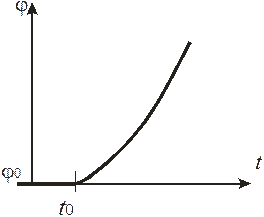
| Рис. 71. Процесс апериодический. Система неустойчива. |
2. р1,2 – комплексные числа
Они получаются при Т1< 2Т2. Тогда подкоренное выражение 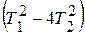 <0.
<0.
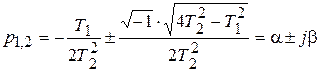 ,
,
где 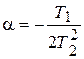 ;
;  ;
; 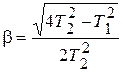 .
.
Решение дифференциального уравнения опять зависит от экспоненты при 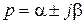
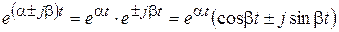 .
.
Наличие 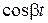 и
и 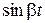 говорит о том, что процесс регулирования будет колебательным, а еat определяет амплитуду колебаний. Следовательно, рост или затухание амплитуды колебаний с течением времени зависит от того, больше или меньше нуля действительная часть a комплексного числа.
говорит о том, что процесс регулирования будет колебательным, а еat определяет амплитуду колебаний. Следовательно, рост или затухание амплитуды колебаний с течением времени зависит от того, больше или меньше нуля действительная часть a комплексного числа.
1. a<0. 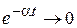 . С течением времени колебания затухают, система устойчива (рис. 72).
. С течением времени колебания затухают, система устойчива (рис. 72).
| Рис. 72. Колебательный процесс регулирования 1 – П, ПД-законы 2 – ПИ, ПИД-законы Системы устойчивы |
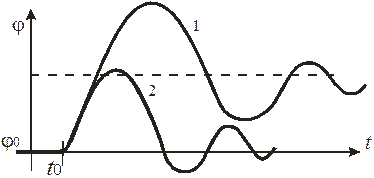
2. a>0. 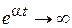 с течением времени амплитуда колебаний растет – системы неустойчива (рис. 73).
с течением времени амплитуда колебаний растет – системы неустойчива (рис. 73).
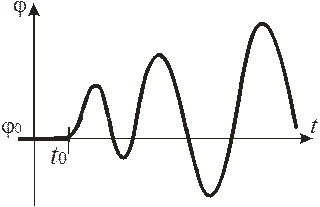
| Рис. 73. Колебательный процесс регулирования. Система неустойчива. |
Если поведение системы описывается дифференциальным уравнением высокого порядка, то общее решение также представлено в виде суммы экспонент
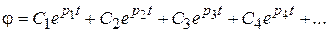
Все предыдущие рассуждения имеют силу и в этом случае, только для всех корней р1, р2, р3, р4, ….
Общее условие устойчивости по корням характеристического уравнения системы:
Для того, чтобы система автоматического регулирования была устойчивой, необходимо и достаточно, чтобы все действительные корни характеристического уравнения системы и все действительные части комплексных корней были отрицательны.
Если хотя бы один из действительных корней или действительная часть одного комплексно-сопряженного корня будут положительны, системабудет неустойчивой.
Если действительная часть комплексно сопряженных корней равны нулю (a=0), система находится на границе устойчивости.
Действительно, тогда
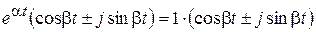 .
.
Система совершает колебания с постоянной амплитудой.
Если система описывается дифференциальным уравнением высокого порядка, то определить его корни решением уравнения невозможно. Для определения устойчивости в этих случаях разработаны критерии устойчивости (алгебраические и частотны).
Дата добавления: 2016-04-11; просмотров: 804;
