Интегрирующие элементы
Различают два типа интегрирующих элементов:
1) идеальный;
2) реальный.
1. Идеальный интегрирующий элемент
Уравнение элемента
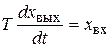 . (7.24)
. (7.24)
Его решение
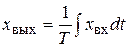 . (7.25)
. (7.25)
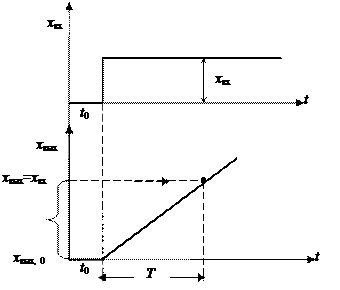
При хвх=const 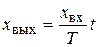 , то есть хвых будет линейно изменяться с течением времени.
, то есть хвых будет линейно изменяться с течением времени.
При t=Т имеем хвых=хвх.
Передаточная функция
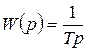 ; (7.26)
; (7.26)
Частотная передаточная функция
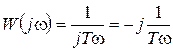 ;
; 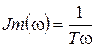 ;
; 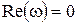 .
.
Частотные характеристики
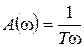 ;
; 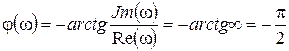 . (7.27)
. (7.27)
| Рис. 29. Разгонная характеристика идеального интегрирующего элемента |
Этот элемент, так же, как и предыдущие, дает запаздывание в прохождении сигнала на фазовый угол j(w). Об этом говорит знак «–» - отрицательные углы j(w).
Примеры: 1) одноемкостные астатические объекты;
2) исполнительные механизмы систем регулирования малой мощности.
2. Реальный интегрирующий элемент
Уравнение
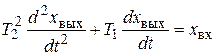 . (7.28)
. (7.28)
Разгонная характеристика
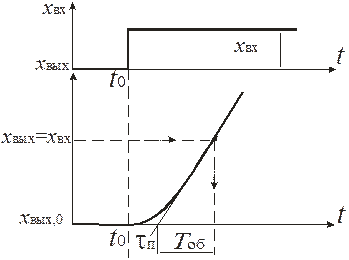
| Рис. 30. Разгонная характеристика реального интегрирующего элемента |
Передаточная функция получается из записи дифференциального уравнения в операторном виде
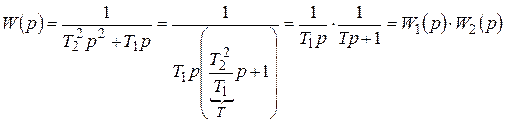 (7.29)
(7.29)
Следовательно, этот элемент является сложным и его можно представить последовательным соединением идеального интегрирующего элемента и апериодического элемента первого порядка с постоянной времени 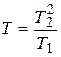 и коэффициентом усиления 1.
и коэффициентом усиления 1.
Частотные характеристики
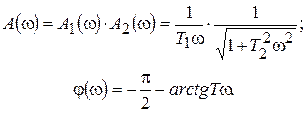 (7.30)
(7.30)
Примером этих элементов может служить двухемкостный астатический объект, представленный на рис. 31.
| Рис. 31. |
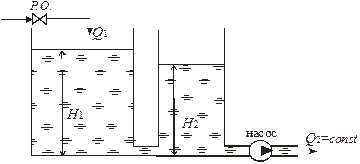
Изменение уровня воды во втором баке Н2 будет происходить по разгонной характеристике (рис. 25).
Дата добавления: 2016-04-11; просмотров: 1026;
