Дифференцирующие элементы
Различают два типа дифференцирующих элементов:
1) идеальный;
2) реальный.
Идеальный дифференцирующий элемент
Такого элемента практически не существует. Он введен как теоретическое понятие, позволяющее упрощать рассмотрение поведения систем регулирования.
Уравнение элемента
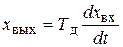 , (7.31)
, (7.31)
где Тд – постоянная времени дифференцирования (время дифференцирования).
Разгонная характеристика элемента
| Рис. 32. Разгонная характеристика идеального дифференцирующего элемента |
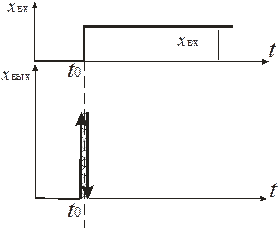
Так как хвх=const до t0 и после t0, то производная в момент времени t0 стремится к ¥ и тут же возвращается в нуль.
Передаточная функция
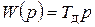 . (7.32)
. (7.32)
Частотные характеристики (р®jw)
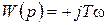 ;
; 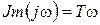 ;
; 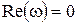 . (7.33)
. (7.33)
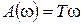 ;
; 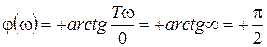 .
.
Следовательно, этот элемент дает опережение сигнала по фазе на угол p/2.
Реальный дифференцирующий элемент
Уравнение
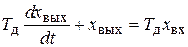 . (7.34)
. (7.34)
Решением этого уравнения является функция 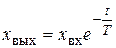 . Отсюда разгонная характеристика элемента
. Отсюда разгонная характеристика элемента
| Рис. 33. Тд – время дифференцирования |

Передаточная функция элемента
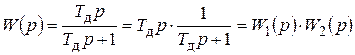 . (7.35)
. (7.35)
Следовательно, реальный дифференциальный элемент можно представить как последовательное соединение идеального дифференцирующего элемента и апериодического элемента первого порядка с постоянной времени Тд и коэффициентом усиления k=1.
Частотные характеристики
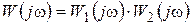
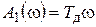 ;
;
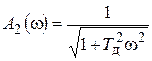 ;
;
 ; (7.36)
; (7.36)
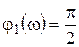 ;
;
 ;
;
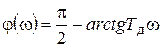 (7.37)
(7.37)
Примеры элемента:
1. Электрическая цепочка, содержащая емкость С и сопротивление R, когда выходной сигнал снимается с сопротивления R.
| Рис. 34. Пример реального дифференцирующего элемента |

2. Элементы с такой электрической цепочкой используются при создании ПИ- закона регулирования (пропорционально-интегрального), включением их в качестве обратной связи регулятора.
3. Эти элементы используются при создании дифференцирующих устройств и динамических связей между регуляторами.
Дата добавления: 2016-04-11; просмотров: 1185;
