Динамические характеристики элементов САР

Для выделения простейших элементов и отличия их друг от друга на вход элементов подают одинаковые типовые сигналы и по реакции элементов, то есть по изменению выходной величины во времени, судят о свойствах элементов и относят их к какому-либо типу.

Основными типами входных сигналов являются: однократное ступенчатое возмущение; однократный импульс и гармонические колебания.

1. Однократное ступенчатое возмущение представляет из себя мгновенное изменение входного сигнала х_вх на какую-то величину. Изменение выходного сигнала х_вых называют кривой разгона или разгонной характеристикой.

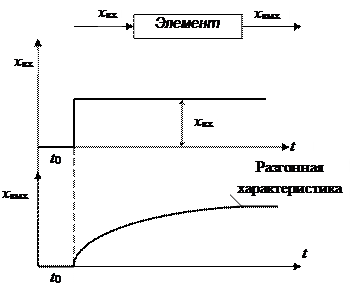
Рис. 20.

Разгонные характеристики являются основным способом экспериментального определения свойств элементов ввиду их наглядности.

2. Однократный импульс представляет из себя мгновенное изменение входного сигнала х_вх на какую-либо величину, выдержки этой величины определенное время t и снятие возмущения. Изменение выходной величины х_вых во времени называют импульсной характеристикой (рис. 19).

Рис. 21.

3. Гармонические колебания представляют из себя изменение входного сигнала х_вх в виде синусоиды. Тогда, через какое-то время, на выходе так же установятся гармонические колебания, но амплитуда их будет другая, и они будут сдвинуты по времени относительно входных колебаний. Если изменять частоту колебаний, то амплитуда выходных колебаний и сдвиг по времени будут зависеть от частоты. Зная амплитуду и частоту входных колебаний и записывая на выходе для каждой частоты амплитуду и сдвиг по времени, получают частотные характеристики элемента, основными из которых являются:

¾ амплитудно-частотная характеристика (АЧХ);

¾ фазо-частотная характеристика (ФЧХ);

¾ амплитудно-фазовая частотная характеристика (АФЧХ).

Если w - частота колебаний, то

;

.

Отношение называют частотной передаточной функцией элемента – W(jw)

. (7.1)

Тогда:

1. Амплитудно-частотная характеристика элемента (АЧХ) равна

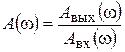(7.2)

2. Фазочастотная характеристика (ФЧХ) - j(w).

3. Амплитудно-фазовая частотная характеристика – W(jw) – это и есть частотная передаточная функция элемента

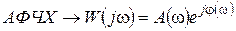(7.3)

Частотную передаточную функцию для частоты w₁ можно представить вектором в полярных координатах или в комплексной плоскости

Re(w) – действительная часть комплексного числа; J_m(w) – мнимая часть комплексного числа.

;

.

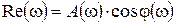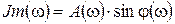; (7.4)

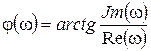. (7.5)

Это основные формулы для расчета частотных характеристик элемента.

Частотные передаточные функции получают из обычных передаточных функций элементов заменой оператора р на jw. Это равносильно переходу от преобразования Лапласа к преобразованиям Фурье.

Типовые динамические элементы

(простейшие элементы)

Различают следующие типы элементов:

1. Позиционные.

2. Интегрирующие.

3. Дифференцирующие.

4. Элементы с запаздыванием.

Рассмотрим эти элементы по следующим характеристикам: уравнение; передаточная функция; частотные характеристики; разгонные характеристики.