Классификация систем автоматического регулирования (САР)
Принята классификация САР по следующим основным признакам:
1) по принципам регулирования;
2) по задачам регулирования;
3) по виду статической характеристики;
4) по характеру работы исполнительного механизма;
5) по количеству входных и выходных величин;
6) по виду дифференциального уравнения САР.
1. По принципу регулирования:
1.1. Принцип Ползунова – Уатта.
1.2. Принцип Понсèле.
1.3. Комбинированный принцип.
1.1. Принцип регулирования Ползунова – Уатта. Это принцип регулирования по отклонению регулируемой величины от заданного значения (принцип сравнения). Структурная схема этого принципа показана на рис. 4. Задача регулятора – устранить отклонения, т.е. 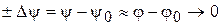 . Поэтому основным достоинством этого принципа является точность регулирования в статических режимах. Недостаток – некачественная работа системы на сложных объектах, обладающих большим временем запаздывания, т.е. промежутком времени от начал перемещения регулирующего органа до начала изменения регулируемого параметра j под влиянием этого перемещения.
. Поэтому основным достоинством этого принципа является точность регулирования в статических режимах. Недостаток – некачественная работа системы на сложных объектах, обладающих большим временем запаздывания, т.е. промежутком времени от начал перемещения регулирующего органа до начала изменения регулируемого параметра j под влиянием этого перемещения.
1.2. Принцип регулирования Понсèле. Его называют регулированием по возмущению l.
| Рис. 5. |

Достоинство принципа – быстрое срабатывание регулятора при нанесении возмущения l на объектах, обладающих большим временем запаздывания (еще до того, как возмущение l окажет влияние на изменения параметра j). Недостаток – грубое регулирование, так как регулируемый параметр j не измеряется.
1.3. Комбинированный принцип. Он подразумевает регулирование по параметру j и возмущению l, то есть объединяет предыдущие принципы регулирования.
Структурная схема
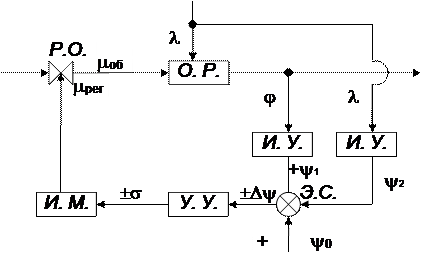
Рис. 6.
Регулятор быстро отрабатывает по возмущению l, а потом производит точное регулирование по параметру j. На практике этот принцип нашел широкое применение.
2. Классификация по задачам регулирования.
По задачам регулирования различают следующие системы:
2.1. системы стабилизации;
2.2. программные;
2.3. следящие (системы соотношений);
2.4. оптимальные (системы экстремального регулирования).
1. Системы стабилизации. Их задача поддерживать среднее значение параметра на заданном значении. Заданное значение j0=const.
К этим системам относятся регуляторы одного параметра: давления, температуры, расхода и т.п.
| ×j0=const t - время |
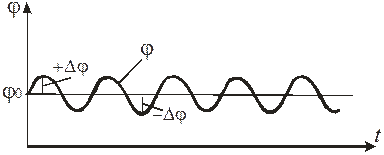
Рис. 7.
2. Программные системы: В этих системах жёстко задана программа изменения параметра j0 по времени t.
| j0 – изменение по программе |
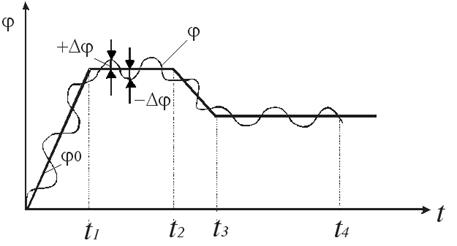
Рис. 8.
Система регулирования изменяет параметр φ так, что его среднее значение изменяется как j0. Примером таких систем являются САР регулирования печей по термообработке металла: в течение времени (0 – t1): - разогрев печи, температура в печи поддерживается постоянной (t1 – t2), затем идёт охлаждение печи (t2 – t3), а потом опять температура поддерживается постоянной (t3 – t4) и.т.д.
3. Следящие системы (системы соотношения). В этих системах один параметр j0 изменяется случайным (произвольным) образом , а второй - j1 должен следить за ним, изменяя таким же образом или в каком-либо соотношении к нему.
| Рис. 9. |
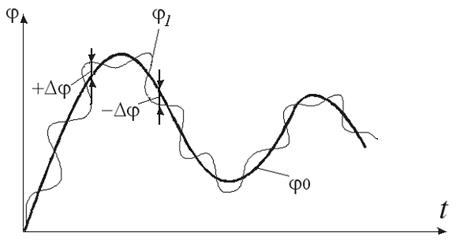
Примером таких систем служат системы регулирования подачи воздуха на сжигание газа в котлах, печах, когда расход газа изменяется произвольным образом.
4. Оптимальные системы. Это более сложный вид систем регулирования. К ним относятся системы, осуществляющие автоматический поиск оптимальных условий ведения процесса. Необходимо каждый раз на конкретном объекте определить критерии оптимальности и строить по нему систему. К критериям оптимальности можно отнести максимальное или минимальное значение какой-либо величины, например минимального расхода энергии на производство какой-либо продукции, обеспечение максимального КПД при работе объекта на разных режимах работы и т.п.
3. Классификация по виду характеристик.
Они подразделяются на два вида:
1) астатические;
2) статические.
Статическая характеристика астатических систем имеет вид:
| Рис. 10. |

Dнеч – зона нечувствительности регулятора, под которой понимается диапазон возможных отклонений параметра, в пределах которых регулятор не работает (не чувствует эти изменения). Из характеристики видно, что среднее значение параметра φ поддерживается равным заданному j0 и не зависит от нагрузки на объект регулирования (mmin¸mmax).
Статическая характеристика статических систем имеет вид
| Рис. 11. |

В статических системах в статических режимах работы регулируемый параметр φ зависит от нагрузки на объект. Каждой нагрузке m соответствует своё значение параметра φ.
Разность (jmax – jmin) называют абсолютной неравномерностью регулятора, а отношение
 (5.1)
(5.1)
называют относительной неравномерностью.
Статические системы работоспособны, если их неравномерность δ = 4 – 8 %.
Разность (j – j0) в статических режимах работы определяет статическую ошибку регулирования ∆jст.
±Djст=( j – j0) (5.2)
4. Классификация по характеру работы исполнительного механизма.Различают следующие системы регулирования:
1) релейные;
2) импульсные;
3) цифровые.
В релейных системах исполнительный механизм работает всё время, пока параметр не входит в пределы зоны нечувствительности Dнеч регулятора.
В импульсных системах исполнительный механизм работает короткими импульсами постоянной длительности, включаясь через равные промежутки времени, пока параметр находится не в пределах зоны нечувствительности регулятора.
В цифровых системах исполнительный механизм работает импульсами разной длительности, которая зависит от величины отклонения параметра от заданного значения, включаясь через равные промежутки времени, пока параметр находится вне пределов зоны нечувствительности регулятора.
5. По количеству входных и выходных величин системы делятся на простые (одномерные), имеющие одну входную и одну выходную величину, и сложные (многомерные), имеющие более двух входных и выходных величин.
6.По виду дифференциального уравнения системы делятся на линейные (их поведение описывается линейными дифференциальными уравнениями) и нелинейными (описываются нелинейными дифференциальными уравнениями)
Дата добавления: 2016-04-11; просмотров: 5856;
