Позиционные элементы.
Подразделяются на следующие виды:
1) пропорциональные;
2) апериодические (инерционные) первого порядка;
3) апериодические (инерционные) второго порядка;
4) колебательные.
Пропорциональный элемент (усилительный)
Уравнение:
хвых=k×хвх, (7.6)
где k – коэффициент усиления.
Передаточная функция
 ;
; 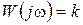 ;
; 
Частотные характеристики
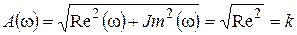 (7.7)
(7.7)
 . (7.8)
. (7.8)
Сдвига по фазе нет.
Разгонная характеристика показана на рис. 23. Она строится по уравнению элемента
| Рис. 23. Разгонная характеристика t0 – момент нанесения возмущения; t – текущее время |

Апериодический (инерционный) элемент первого порядка
Дифференциальное уравнение элемента:
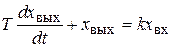 ; (7.9)
; (7.9)
где k – коэффициент усиления; Т – постоянная времени.
| Рис. 24. Разгонная характеристика |
 Разгонная характеристика получается из решения дифференциального уравнения элемента
Разгонная характеристика получается из решения дифференциального уравнения элемента
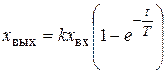 . (7.10)
. (7.10)
Следовательно, разгонная характеристика элемента представляет собой экспоненту. Постоянная времени Т представляет собой отрезок времени, отсекаемый проекцией касательной, проведенной к кривой разгона в начальной точке при t0. При t=¥ хвых устанавливается на новом значении хвых,уст. Уравнение статики элемента получается из дифференциального уравнения,
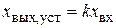 ,
,
из которого легко получают коэффициент усиления k по экспериментальным данным.
Передаточная функция получается из дифференциального уравнения
 . (7.11)
. (7.11)
Частотная передаточная функция получается заменой оператора р на jw

где  ;
; 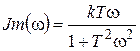 .
.
Амплитудно-частотная характеристика

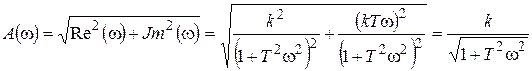 ; (7.12)
; (7.12)
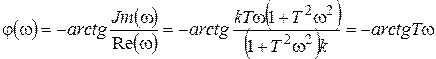 . (7.13)
. (7.13)
При частоте w, изменяющейся от 0 до ¥ А(w) изменяется от k до 0, а j(w) ® от 0 до (-p/2). Отрицательное значение j(w) означает, что в элементе происходит запаздывание в прохождении сигнала.
Примеры этого элемента:
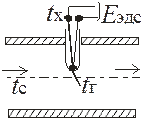
1) одноемкостные статические объекты (рис. 25а);
2) термопары и термометры сопротивления (рис. 25б);
3) электрическая цепь, содержащая емкость и электрическое сопротивление (рис. 25в).

| 
| 
| ||
| а) | б) | в) | ||
Рис. 25. Примеры инерционных элементов первого порядка:
а – одноемкостный статический объект регулирования уровня воды; б – термопара;
в – электрическая цепочка сопротивление R – емкость C
Апериодический (инерционный) элемент второго порядка
Дифференциальное уравнение элемента:
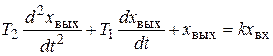 . (7.14)
. (7.14)
При определенном соотношении коэффициентов Т1 и Т2 получим апериодический элемент второго порядка. Корни уравнения – действительные числа. Операторный вид уравнения:
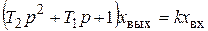 .
.
Характеристическое уравнение
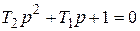 . (7.15)
. (7.15)
Его корни получаются из решения этого квадратного алгебраического уравнения
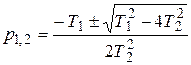 , где р1,2 – действительный числа при соотношении Т1>2Т2. Это условие соотношения коэффициентов, при котором корни уравнения (6.38) являются действительными числами. .
, где р1,2 – действительный числа при соотношении Т1>2Т2. Это условие соотношения коэффициентов, при котором корни уравнения (6.38) являются действительными числами. .
Разгонная характеристика элемента
| Рис. 26. Разгонная характеристика инерционного элемента второго порядка |

При замене этого элемента на апериодический элемент 1го порядка, в точке перегиба кривой разгона проводят касательную, ограниченную начальным значением хвых,0 и его конечным значением хвых,уст. Подкасательная (проекция касательной на ось времени) численно равна постоянной времени Т. Промежуток времени от t0 до начал отсчета постоянной времени Т называют переходным запаздыванием tп.
Передаточная функция элемента получается из уравнения, записанного в операторном виде
 . (7.16)
. (7.16)
Полином по р в знаменателе может быть разложен на множители. Тогда
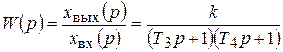 ; (7.17)
; (7.17)
где Т3 и Т4 – новые постоянные времени. Связь постоянных времени 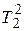 и Т1 с Т3 и Т4 получается раскрытием скобок в знаменателе передаточной функции
и Т1 с Т3 и Т4 получается раскрытием скобок в знаменателе передаточной функции  ;
;  .
.
Тогда передаточную функцию апериодического элемента 2-го порядка можно представить в виде
 . (7.18)
. (7.18)
То есть, этот элемент может быть представлен последовательным соединением двух апериодических элементов 1-го порядка с постоянными времени Т3 и Т4 и коэффициента усиления k и 1.
Такое представление упрощает получение частотных характеристик апериодического элемента 2-го порядка

 ;
;
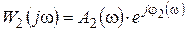
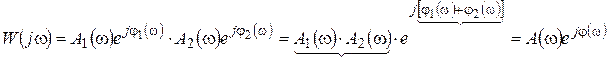 .
.
Следовательно, АЧХ будет
 , (7.19)
, (7.19)
а ФЧХ –
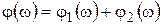 . (7.20)
. (7.20)
 ;
;
 ;
;
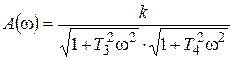 ; (7.21)
; (7.21)
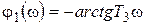 ;
; 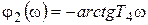 ;
; 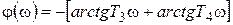 . (7.22)
. (7.22)
Этот метод позволяет легко определить АЧХ и ФЧХ сложных элементов, которые могут быть представлены последовательным соединением простейших элементов.
Колебательные элементы
Уравнение элемента
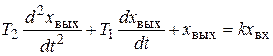 .
.
Корни этого уравнения – комплексные числа. Соотношения между постоянными времени Т1 и Т2 следует из решения характеристического уравнения
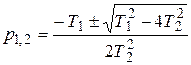 .
.
При Т1 < 2Т2 имеем комплексные корни
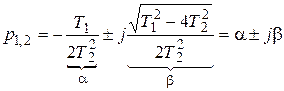 . (7.23)
. (7.23)
Из этого следует, что процесс изменения хвых во времени будет колебательным
Разгонная характеристика
| Рис. 27. Разгонная характеристика колебательного элемента |

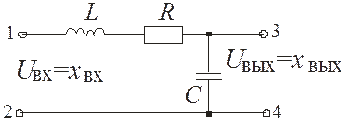
Примером колебательных элементов могут служить пневматические, гидравлические и электрические демпферы (гасители колебаний). На рис. 28 показана электрическая цепочка, состоящая из индуктивности L, сопротивления R и емкости С.
| Рис. 28. Пример колебательного элемента |
Дата добавления: 2016-04-11; просмотров: 1112;
