Объемное расширение твердых тел

При нагревании объем твердого тела изменяется по закону

V = V₀(1 + bt°),

где V – объем при t = t °C; V₀ – объем при t = 0 °С; t° – температура; b – температурный коэффициент объемного расширения, [b] = = 1/°С.

Утверждение. Между температурным коэффициентом объемного расширения и температурным коэффициентом линейного расширения существует соотношение

b = 3a. (1.9)

Почему это так?

Рассмотрим куб с ребром l₀, начальный объем которого . Нагреем куб от 0 °С до температуры t °С. Тогда его объем при температуре t °С составит

V(t°) = l³(t) = [l₀(1 + at)]³ =

.

Поскольку a ~ 10^–5, то членами 3a²t² и a³t³ мы пренебрегли. Тогда

V = V₀(1 + 3at) = V₀(1 + bt), где b = 3a.

Заметим, что поскольку b = 3a ~ 10^–5, можно пользоваться приближенной формулой

V(t₂) = V(t₁)[1 + b(t₂ – t₁)], (1.10)

где V(t₁) – объем при температуре t₁; V(t₂) – объем при температуре t₂.

Зависимость площади поверхности твердого тела

От температуры

При нагревании площадь поверхности твердого тела изменяется по закону

S = S₀(1 + gt°), (1.11)

где S – площадь поверхности тела при температуре t °С; S₀– площадь поверхности телапри температуре t = 0°С;g – температурный коэффициент увеличения площади, [g] = 1/°С; t° – температура (°С).

Для всех твердых тел g = 2a, где a – температурный коэффициент линейного расширения.

Почему это так?

Рассмотрим квадратную пластину со стороной l₀, начальная площадь которой . Нагреем ее от 0 °С до температуры t °С. Тогда площадь пластины при температуре t °С составит

S(t°) = l²(t) = [l₀(1 + at)]² = .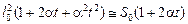

Поскольку a ~ 10^–5, то членом a²t² мы пренебрегли. Тогда

g = 2a.

Справедлива формула, аналогичная формуле (1.10):

S(t₂) @ S(t₁)[1 + g(t₂ – t₁)], (1.12)

где S(t₁) – площадь при температуре t₁; S(t₂) – площадь при температуре t₂.

СТОП! Решите самостоятельно: А9, А11, В8, В13.