Задачи средне трудности

В1. Как должны относиться длины l₁ и l₂ двух стержней из материалов с различными коэффициентами линейного расширения b₁ и b₂, чтобы при любой температуре разность длин стержней оставалась постоянной?

В2.Два одинаковых стальных моста должны быть построены один на севере, другой – на юге. Каковы должны быть при 0 °С зазоры, компенсирующие удлинение моста при изменении температуры, если на юге возможны коле­бания от –10 до +50 °С, а на севере от –50 до +20 °С? При 0 °С длина моста L₀= 100 м, коэффициент линейного расширения стали b = 1×10^–5 1/°C.

В3. При температуре 0 °С железный стержень имеет длину 20 см,а алюминиевый – на 10 см меньше. Какой будет разность длин этих стержней при температуре t °С? Коэффициент линейного расширения железа равен 12×10^–6 1/°C,а алюминия – 24×10^–6 1/°C.

В4. В центре стального диска имеется отверстие диаметром 4,99 мм(при 0 °С). До какой температуры следует нагреть диск, чтобы в отверстие начал прохо­дить шарик диаметром 5,00 мм? Линейный коэффици­ент теплового расширения стали a = 1,1×10^–5 1/°C.

В5. Какую силу F надо приложить к стальному стержню сечением S = = 1,0 см², чтобы растянуть его на столько же, насколько он удлиняется при нагревании на Dt = 1,0 °С? Коэффициент линейного расширения a = 12×10^–6 1/°C. Модуль Юнга Е = 2,1×10¹¹ Па.

В6. При температуре t₀ = 0 °С длины алюминиевого и железного стержней l_a0 = 50,00 см и l_ж0 = 50,05 см. Сечения стержней одинаковы. При какой температуре t₁ длины стержней и при какой температуре t₂ их объемы будут одинаковы? Коэффициенты линейного расширения алюми­ния и железа: a_а = 2,4×10^–5 1/°C, a_ж = 1,2×10^–5 1/°C.

В7. Масса спирта, взятого при 0 °С в объеме 500 см³, равна 400 г. Определить плотность спирта при 15 °С.

В8. Латунный сосуд при нагревании увеличился в объеме на п = 0,6 %. Найти увеличение температуры Dt сосуда, если коэффици­ент линейного расширения латуни a = 2×10^–5 1/°C.

В9. В кварцевый литровый сосуд диаметра d = 6 см до половины налили воду, а затем положили шар из эбонита, имеющий объем V = 100 см³. На какую высоту Dh подни­мется уровень воды при изменении температуры от t₁ = 10 °С до t₂= 70 °C? Коэффициент объемного расширения воды a = 3×10^–4 1/°C, коэффициент линейного расширения эбонита b = 8×10^–5 1/°C. Тепловым расширением кварца пренебречь.

В10. Пузырьковый уровень представляет собой слегка изог­нутую трубку, заполненную жидкостью так, что остается очень маленькое пространство – пузырек, в котором находятся пары жидкости. Когда пузырек больше: летом или зимой?

В11.Нефть содержится в железной цилиндрической цистерне, высота которой 6 м, а диаметр основания 5 м. При температуре 0 °С нефть не доходит до краев цистерны на 20 см. При какой температуре нефть начнет пере­ливаться через край цистерны? Учесть тепловое расширение цистерны.

B12. Железный бак вмещает 50 л керосина при 0 °С. Сколько керосина выльется из бака, если его внести в комнату с температурой 20 °С?

В13. В цилиндрический открытый сосуд налита неиспаряющаяся жидкость. При температуре t₀ = 0 °С давление на дно сосуда равно р₀. Найти давление на дно сосуда при температуре t, если температурный коэффициент линейного расширения материала сосуда равен a. Уровень жидкости остается все время ниже края сосуда.

В14. Коэффициенты объемного расширения воды для трех интервалов температур:

a₁ = –3,3×10^–5 1/°C (0 £ t₁ £ 4 °С);

a₂ = 4,8×10^–5 1/°C (4 £ t₂ £ 10 °С);

a₃ = 1,5×10^–4 1/°C (10 £ t₃ £ 20 °С).

Найти объем воды V при температуре t = 15 °С, если при температуре t' = 1 °C объем V' =1,000×10³ см³.

В15. Какова температура воды в водоемах под слоем льда?

Задачи трудные

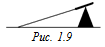С1. Если нагретую мед­ную лопатку положить на брусок свинца треугольного сечения (рис. 1.9), то можно явственно услышать звук. Объясните природу возникно­вения этого звука.

С2. Стержень длиной l₁ сделан из материала с коэффициентjм линейного расширения a₁, а стержень длиной l₂– изматериала с коэффициентом линейного расширения a₂. Стержни спаяли, и получился стержень длиной l₁ + l₂. Каков его коэффициент линейного расширения?

С3. Стальная и бронзовая пластинки толщиной 0,2 мм каждая склепаны на концах так, что при температуре 20 °С образуют плоскую биметаллическую пластинку. Каков будет радиус изгиба этой биметаллической пластинки при температуре 120 °С? Коэффициент линейного расширения стали a₁ = 1×10^–5 1/°C, бронзы a₂ = 2×10^–5 1/°C.

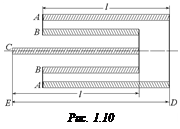
С4.Центральный стержень С и внешняя оболочка А этало­на длины (рис. 1.10) имеют температурный коэффициент линейного расширения a₁. Их длины при 20 °С одинаковы и равны l. Температурный коэффициент линейного расширения внутренней трубы В равен a₂. Какой должна быть длина L внутренней трубы В при 20 °С, чтобы тепловое расширение не меняло полной длины эталона ED?

С5. Разность длин алюминиевого и медного стержней при любой температуре составляет 15 см. Какую длину при 0 °С будут иметь эти стержни?

С6. Между двумя стенками помещен стержень по­стоянного сечения S, состоящий из двух частей одина­ковой длины l/2, имеющих коэффициент теплового рас­ширения a₁ и a₂и модули Юнга Е₁ и Е₂ соответственно. При температуре Т₁ торцы стержня лишь касаются сте­нок. С какой силой стержень будет давить на стенки, и насколько сместится место стыка частей стержня, если стержень нагреть до температуры Т₂? Деформацией стенок пренебречь.

С7.Бронзовый стержень был охлажден в жидком азоте до температуры –201 °С. Охлажденный стержень плотно вставили в прямоугольное отверстие жесткой обоймы, имеющей температуру 20 °С так, что зазор между торцами стержня и соответствующими плоско­стями отверстия обоймы можно считать равным нулю. Каким стало давление стержня на обойму после того, как он нагрелся до температуры 20 °С? Коэффициент линейного расширения бронзы a₂ = 1,75×10^–5 1/°C,модуль Юнга Е = 1,04×10¹¹ Па.

С8. Латунное кольцо сечением 2×5 мми диаметром в несколько сантиметров было нагрето до температуры 300 °С и плотно надето на стальной цилиндр, имеющий температуру 18 °С. Какое усилие на разрыв испытывает кольцо после охлаждения до 18 °С? Коэффициент ли­нейного расширения латуни a₂ = 1,84×10^–5 1/°C. Модуль Юнга Е = =6,47×10¹⁰ Па.

С9. В кварцевый сосуд объема V₁ = 2,5 лпомещен ла­тунный цилиндр массы т₂ = 8,5кг. Остальная часть со­суда заполнена водой. При нагревании сосуда вместе с со­держимым на Dt = 3 °С уровень воды в сосуде не изменился. Найти коэффициент объемного расширения воды b. Коэффициенты линей­ного расширения кварца и латуни: a₁ = =0,42×10^–6 1/°C и a₂ = 0,2×10^–4 1/°C. Плот­ность латуни r₂ = 8,5×10³ кг/м³.

С10.Найти объем шарика ртутного термометра, если известно, что при температуре t₀= 0 °С ртуть заполняет только шарик, а между делениями 0 и 100 °С объем канала V = 3 мм³. Коэффициент объемного расширения ртути a₂ = 1,8×10^–4 1/°C, коэффициент линейного расширения стек­ла b = 8×10^–6 1/°C.

С11. Цилиндрический алюминиевый сосуд с ртутью нагрели на 100 °С. На сколько процентов увеличилась высота столба ртути? Коэффициент линейного расширения алюминия равен 24×10^–6 1/°C, а коэффициент объемного расширения ртути – 18 ×10^–5 1/°C.

С12. Кусок меди погружен в воду. На сколько процентов из­менится действующая на него выталкивающая сила, если нагреть его и воду на 40 °С?

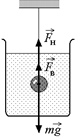Рис. 1.11

Коэффициент линейного расширения меди равен 17×10–6 1/°C, коэффициент объемного расширения воды считать равным 15×10–5 1/°C. С13. Стальной шарик массой 100 г опущен на нити в керосин. Как изме­нится сила натяжения нити, если всю систему нагреть от 20 до 50 °С (рис. 1.11)? С14. В два сосуда конической формы, расширяющихся кверху и книзу, и цилиндрический налита вода при температуре t = 100 °С. Как изменится давление на дно сосудов после охлаждения воды до комнатной температуры?

С15.B одном из двух сообщающихся сосудов, на­полненных жидкостью при 10 °С до уровня Н₀ = 10 см, температура жидкости поднялась на Dt = 6 °С. Какая воз­никнет при этом разность уровней, если объемный коэф­фициент расширения жидкости b = 0,0026 1/°C? Рас­ширением сосуда можно пренебречь.

С16. Сообщающиеся сосуды заполнены жидкостью, имею­щей температуру t₁. При нагревании жидкости в одном из сосудов до температуры t₂ уровень жидкости в этом сосуде установился на высоте Н, а в другом – на высоте h. Найти коэффициент объемного расширения жидкости.

С17. В колбу, плотно закрытую пробкой со вставленной в нее трубкой, до самой пробки налит керосин (рис. 1.12). Как изменится давление на дно колбы при нагревании керосина на Dt = 30 °С, если объем колбы V = 2 л, ее высота h = 20 см, сечение трубки S = 2 см2? Тепловым расширением пренебречь. C18. В одном колене сообщающихся сосудов темпера­тура 10 °С, в другом 80 °С. Уровень керосина в одном колене

Рис. 1.12

280 мм, а другом – 300 мм. Найти коэффициент объемного расширения керосина.