ЗАКОН БОЙЛЯ–МАРИОТТА
Экспериментально установлено, что для газов в достаточно широком диапазоне температур справедлив закон:
При постоянной температуре для данной массы газа произведение давления газа на его объем есть величина постоянная:
pV = const.
Этот закон назван законом Бойля–Мариотта. Он описывает изотермический процесс.
Процессы, при которых температура газа остается неизменной, называются изотермическими.
Заметим, что при очень низких температурах и при очень высоких давлениях этот закон не выполняется.
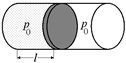
Задача 2.1. Найти давление в цилиндре (рис. 2.1,а), если поршень сместить: 1) на l/2 влево; 2) на l/2 вправо (рис. 2.1,б). Начальное давление газа р0.
| р0 | 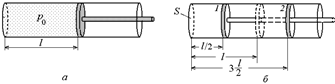 Рис. 2.1
Рис. 2.1
|
| р1 = ? р2 = ? | |
Решение. При неподвижном поршне V0 = lS, где S – площадь основания цилиндра.
1. При сдвиге поршня влево (рис. 2.1,б) р0V0 = р1V1, V1 = 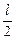 S. Тогда p0lS =
S. Тогда p0lS = 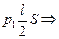 р1 = 2р0.
р1 = 2р0.
2. При сдвиге поршня вправо V2 = 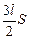 . Тогда
. Тогда
р0V0 = р2V2 Þ p0lS = 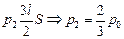 .
.
Ответ: 1) р1 = 2р0; 2) 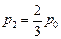 .
.
СТОП! Решите самостоятельно: А1–А5, А7.
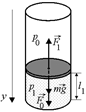
Задача 2.2. В горизонтально расположенном цилиндре с площадью основания S, заполненном воздухом при атмосферном давлении р0, на расстоянии l от дна находится поршень массой т, плотно прилегающий к стенкам цилиндра (рис. 2.2,а). Поршень может без трения перемещаться по цилиндру. На каком расстоянии от дна сосуда будет находиться поршень, если сосуд расположить: 1) вертикально днищем вниз (рис. 2.2,б); б) вертикально днищем вверх (рис. 2.2,в); 3) под углом a к вертикали днищем вниз (рис. 2.2,г)?
| S; т; l; р0; a | Решение. 1. Поскольку поршень неподвижен, равнодействующая сил, действующих на него, равна нулю: |
| l1, l2, l3 = ? | |
F0 + mg – F1 = 0,
где F1 = р1S, F0 = p0S – силы давления воздуха снизу и сверху.
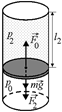
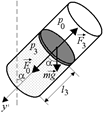
а б в г
Рис. 2.2
Согласно закону Бойля–Мариотта
р0V0 = р1V1 Þ p0lS = p1l1S.
Получаем систему уравнений
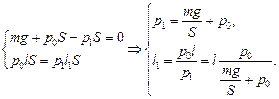 Þ
Þ 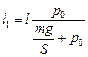 .
.
2. Рассуждая аналогично, получаем систему уравнений
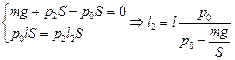 .
.
3. В данном случае нам необходимо записать уравнение второго закона Ньютона в проекции на наклонную ось у¢, направленную вдоль оси цилиндра (см. рис. 2.2,г). Получим
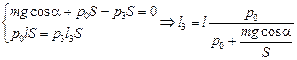 .
.
Ответ: 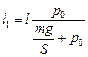 ;
; 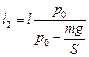 ;
; 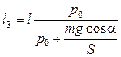 .
.
СТОП! Решите самостоятельно: В13, С2.
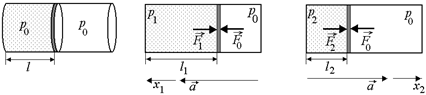
Задача 2.3. В горизонтально расположенном цилиндре с площадью основания S, заполненном воздухом при атмосферном давлении р0, на расстоянии l от дна находится поршень массой т, плотно прилегающий к стенкам цилиндра (рис. 2.3,а). Сосуду сообщают ускорение а: 1) влево (рис. 2.3,б); 2) вправо (рис. 2.3,в). Найти давление воздуха в сосуде и расстояние от поршня до дна сосуда.
а б в
Рис. 2.3
| S; т; l; р0; а | Решение. 1. По второму закону Ньютона в проекции на ось х1: F0 – F1 = та, а закон Бойля–Мариотта: р0V0 = р1V1 Þ p0lS = p1l1S. |
| l1, р1, l2, р2 = ? | |
Получаем систему уравнений
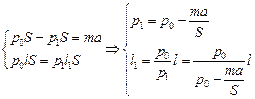 Þ
Þ 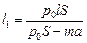 .
.
2. По второму закону Ньютона в проекции на ось х2: F2 – F0 = = та, а закон Бойля–Мариотта: p0lS = p2l2S. Получаем систему уравнений
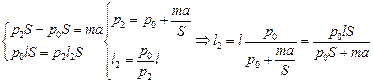 .
.
Ответ: 1) 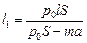 ; 2)
; 2)  .
.
СТОП! Решите самостоятельно: С13, С14, С17.
Задача 2.4. Два поршня площадями S1 и S2, скрепленные жестким стержнем длиной 2l, находятся в трубе (рис. 2.4) при давлении р0. Определить: 1) каким должно быть давление воздуха между поршнями, чтобы они были неподвижны; 2) на сколько сместятся поршни и в каком направлении, если давление в трубе повысится до величины р1 > р0.
| S1 S2 l р0 р1 | Рис. 2.4 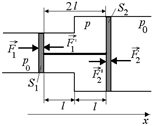
|
| 1) р = ? 2) х = ? | |
Решение. 1. Поскольку поршень неподвижен, то равнодействующая сил равна нулю: 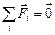 ,
, 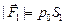 ,
, 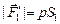 ,
, 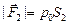 ,
, 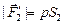 . В проекции на ось х второй закон Ньютона примет вид
. В проекции на ось х второй закон Ньютона примет вид
р0S1 – pS1 + pS2 – p0S2 = 0 Þ p(S2 – S1) = p0(S2 – S1).
Тогда р = р0 (если S2 – S1 ¹ 0).
Чтобы система осталась в равновесии при повышении внешнего давления, необходимо, чтобы давление между поршнями стало таким же, как и снаружи.
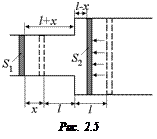 2. Чтобы давление между поршнями повысилось, объем по закону Бойля–Мариотта должен уменьшиться, т.е. поршни должны сместиться влево (рис. 2.5). Тогда р0V0 = рV1, где
2. Чтобы давление между поршнями повысилось, объем по закону Бойля–Мариотта должен уменьшиться, т.е. поршни должны сместиться влево (рис. 2.5). Тогда р0V0 = рV1, где
V0 = S2l + S1l, V1 = S2(l – x) + S1(l + x).
Отсюда
(S2l + S1l)р0 = р[S2(l – x) + S1(l + x)] =
= р[S2l + S1l – S2x + S1x].
Введем V0 = S2l + S1l – начальный объем газа, тогда
V0p0 = p[V0 – x(S2 – S1)] Þ V0p0 = pV0 – px(S2 – S1) Þ
Þ px(S2 – S1) = V0(p – p0) Þ
Þ 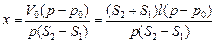 .
.
Ответ: 1) р = р0; 2) 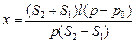 .
.
Читатель: Если в последней формуле положить S2 = S1, то получим ноль в знаменателе. Что же получается: х ® ¥?! Как это понять?
Автор: Вспомним, с чего мы начинали решение задачи: 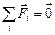 Þ Þ p(S2 – S1) = p0(S2 – S1), если S2 – S1 ¹ 0 Þ р = р0, если S2 – S1 = 0, то это равенство примет вид р×0 = р0×0, а оно верно при любом р. Это значит, что в трубе с постоянным сечением система будет в равновесии при любом внешнем давлении!
Þ Þ p(S2 – S1) = p0(S2 – S1), если S2 – S1 ¹ 0 Þ р = р0, если S2 – S1 = 0, то это равенство примет вид р×0 = р0×0, а оно верно при любом р. Это значит, что в трубе с постоянным сечением система будет в равновесии при любом внешнем давлении!
СТОП! Решите самостоятельно: С19–С21.
Поршневой насос
Задача 2.5. В сосуде объемом V при давлении р0 находится газ, который начинают откачивать с помощью поршневого насоса с рабочей камерой объемом V1 (рис. 2.6). Найти давление газа рп после п ходов поршня.
| V; V1; р0; п | Решение. Читатель: При п ходах поршня объем газа п раз увеличивается на объем V1, поэтому запишем уравнение Бойля–Мариотта в виде | |
| рп = ? | ||
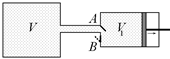 Рис. 2.6
Рис. 2.6
| р0V = pn(V + nV1) Þ 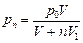 .
Автор: К какой массе газа относится запись? .
Автор: К какой массе газа относится запись?
| |
Читатель: К массе, которая была в сосуде.
Автор: Но ведь уже после первого хода часть этой массы уходит из системы: когда поршень начинает движение справа налево, он закрывает клапан А и открывает клапан В, через который газ и покидает систему. Масса газа меняется!
1-й ход: р0V = p1(V +V1) (для исходной массы газа). Потом газ, находящийся в рабочей камере, уходит наружу, и в сосуде остается меньшая масса газа при давлении 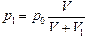 . Для этой оставшейся массы при последующем ходе справедливо р1V = p2(V+V1), где р2 – давление после 2-го рабочего хода и т.д.:
. Для этой оставшейся массы при последующем ходе справедливо р1V = p2(V+V1), где р2 – давление после 2-го рабочего хода и т.д.:
| р2V = p3(V +V1) р3V = p4(V +V1) ………………….. рп–1V = pп(V +V1) | 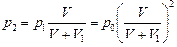
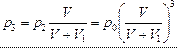
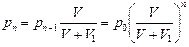
|
Ответ: 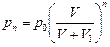 .
.
СТОП! Решите самостоятельно: С5, С6, С39.
Дата добавления: 2016-04-11; просмотров: 1722;
