Перевернутый стакан

Задача 2.7.Тонкостенный стакан массы М и объема V₀ ставят вверх дном на поверхность воды и медленно опускают вглубь так, что он все время остается вертикальным (рис. 2.8). Плотность воды r, атмосферное давление р_а, температура постоянна. Определить: 1) зависимость давления р воздуха в стакане от глубины погружения h; 2) объем воздуха в стакане на глубине h; 3) величину силы Архимеда F_A на глубине h; 4) глубину h_min, начиная с которой стакан уже не всплывает на поверхность.

М; V0; ра; h; r	Решение. 1. Давление на глубине h составляет р = ра + rgh (размерами стакана мы пренебрегаем). 2. Воспользуемся законом Бойля–Мариотта. Если вначале погружения в стакане находился воздух объемом V0 при атмосферном давлении, то на глубине h в стакане находится объем воздуха V при давлении р: раV0 = pV. Отсюда 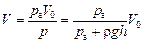. 3. Вычислим силу Архимеда, учитывая, что объем вытесненной воды равен объему воздуха в стакане V:
р = ? V = ? FA = ? hmin= ?
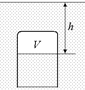Рис. 2.8

.

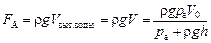4. Критическую глубину h_min, начиная с которой стакан уже не всплывет, найдем из условия равенства силы Архимеда и силы тяжести: F_A = Mg. При дальнейшем погружении величина силы Архимеда будет меньше силы тяжести, и стакан самостоятельно всплыть уже не сможет:

.

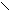
Ответ: 1) р = р_а + rgh; 2) ;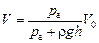

3) ; 4) .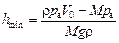

СТОП! Решите самостоятельно: С7, С8, С13.