Объемного расширения для некоторых жидкостей
| Жидкость | b, 1/°С | Жидкость | b, 1/°С |
| Ртуть Вода (t° > 20 °С) Серная кислота | 0,18×10–3 0,30×10–3 0,56×10–3 | Нефть, керосин Спирт Эфир | 1,0×10–3 1,1×10–3 1,7×10–3 |
СТОП! Решите самостоятельно: А10, В7, В12.
Задача 1.3. Цилиндрический сосуд наполнен жидкостью объемом Vж = 10 см3 с коэффициентом объемного расширения bж = =1×10–3 1/°С. В сосуд положили кусок металла объемом Vт = 10 см3 с коэффициентом объемного расширения bт = 1×10–4 1/°С. Сосуд нагревают на Dt = 10 °С. На сколько поднимется уровень жидкости, если площадь дна сосуда S = 10 см2? Температурным расширением сосуда пренебречь.
| Vж = 10 см3 = 10×10–6 м3 bж = 1×10–3 1/°С Vт = 10 см3 = 10×10–6 м3 bт = 1×10–4 1/°С Dt = 10 °С S = 10 см2 =10×10–4 м2 | 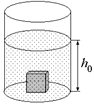 Рис. 1.5 Рис. 1.5
|
| F = ? |
Решение. Сначала высота столба жидкости (рис. 1.5) определялась соотношением
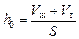 .
.
После подъема температуры на Dt высота увеличилась до значения
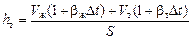 .
.
Мы должны найти величину Dh = hт – h0. Нетрудно получить
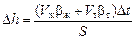 .
.
Подставим численные значения:
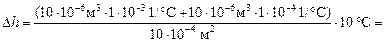
= 1,1×10–4 м » 0,1 мм.
Ответ: 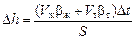 » 0,1 мм.
» 0,1 мм.
СТОП! Решите самостоятельно: В9, В11.
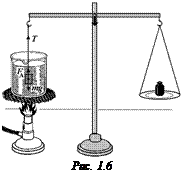 Задача 1.4. На весах уравновешено тело, погруженное в сосуд с жидкостью. Как изменится равновесие весов, если жидкость нагреть?
Задача 1.4. На весах уравновешено тело, погруженное в сосуд с жидкостью. Как изменится равновесие весов, если жидкость нагреть?
Решение. Сила натяжения нити (рис. 1.6) равна
T = mg – FA.
Определим, как изменится сила Архимеда. Пусть rж0 – плотность жидкости в начальный момент, а rж – плотность жидкости после нагрева. Тогда в начальный момент
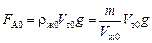 ,
,
где Vж0 – начальный объем жидкости; Vт0 – начальный объем тела. После нагревания получаем
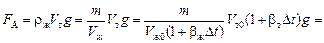
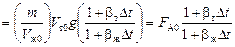 .
.
Ответ: 1) если bт > bж, то FА увеличится и груз перетянет;
2) если bт < bж, то FА уменьшится и тело перетянет.
(Напомним, что обычно bт < bж.)
Задача 1.5. В цилиндрический сосуд налита жидкость массы т с коэффициентом объемного расширения b > 0. Как изменится давление на дно сосуда при нагревании, если: 1) коэффициентом линейного расширения сосуда можно пренебречь; 2) a > 0?
| т; b; a | Решение. 1. Пусть Dt > 0. Масса жидкости не изменилась! Следовательно, вес жидкости остался тот же, давление |
| Dр = ? | |
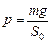 осталось неизменным, так как S0 не изменилась. Значит,
осталось неизменным, так как S0 не изменилась. Значит, 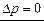 .
.
2. Пусть Dt > 0. Тогда S(t) = S0(1 + 2aDt). Вес жидкости равен mg, следовательно, давление равно
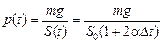 ,
,
 .
.
То есть давление уменьшилось.
Ответ: 1) давление не изменится; 2) давление уменьшится.
СТОП! Решите самостоятельно: В13, С12, С14.
Задача 1.6. Сосуд имеет форму, показанную на рис. 1.7,а. Площадь его нижней части S0, а верхней S1. Высота нижней части h0. В сосуд налили жидкость, полностью заполнив его нижнюю часть. Коэффициент объемного расширения жидкости b, плотность r0. На сколько изменится давление жидкости на дно сосуда, если ее нагреть на Dt °С? Тепловым расширением сосуда пренебречь.
| h0 S0; S1 Dt °С b; r0 | Решение. Сначала давление жидкости было равно р0 = r0gh0. После нагревания (рис. 1.7,б)
р1 = r(t)gh1 = 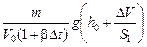 , ,
|
| Dр = ? |
где V0 – начальный объем жидкости; DV – увеличение объема жидкости.
Рис. 1.7 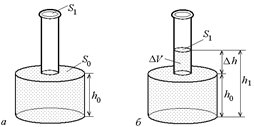
Учитывая, что
DV = bV0Dt =b(S0h0)Dt, а т/V0 = r0,
получим
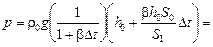
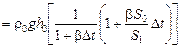 .
.
Полученная формула слишком громоздкая и при желании ее можно заменить более простой:
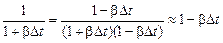 .
.
Тогда
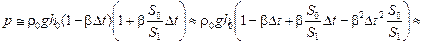
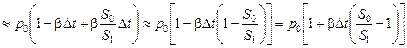 .
.
Теперь вычислим интересующее нас изменение давления жидкости на дно:
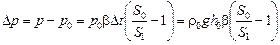 .
.
Ответ:  .
.
СТОП! Решите самостоятельно: С15, С17.
Дата добавления: 2016-04-11; просмотров: 1233;
