Закон Гука и модуль Юнга

Прежде чем решать следующую задачу, поговорим о силах, которые возникают при попытках сжать или растянуть металлические стержни.

Деформации растяжения и сжатия.Если к однородному, закрепленному с одного конца стержню приложить силу 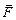вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения (рис. 1.1). Де­формацию при этом характеризуют абсолютным удлинением Dl = l – l₀ и относительным удлинением 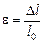, где l₀ – начальная длина, а l – конечная длина стержня. При малых деформа­циях (|Dl| << l₀)большинство тел проявляет упругие свойства.

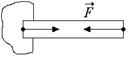
Рис. 1.1 Рис. 1.2

Деформацию растяжения испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами и т. д.

Если на закрепленный стержень подействовать силой вдоль его оси по направлению к стержню (рис. 1.2),то он подвергнется сжатию. В этом случае относительное удлинение (относительная деформация) e отрицательна (e < 0). Деформацию сжатия испытывают столбы, колонны, стены, фундаменты зданий и т. п.

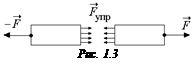Напряжение.В любом сечении деформируемого тела действуют силы упру­гости, препятствующие разрыву тела на части (рис. 1.3). Дефор­мированное тело находится в напря­женном состоянии, которое характе­ризуется особой величиной, называе­мой механическим напря­жением или короче – напря­жением.

Напряжение – величина, равная отношению модуля силы упругости к площади поперечного сечения¹ тела:

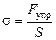, (1.3)

где s – напряжение; F_yпp – модуль силы упругости; S – площадь поперечного сечения.

_______________

¹Сечение тела производится плоскостью, перпендикулярной на­правлению силы упругости. При этом предполагается, что деформа­ция тела во всех участках сечения одинакова.

В СИ за единицу напряжения принимается паскаль (Па):

1 Па = 1 Н/м².

Заметим, что в формуле (1.3)иногда удобно модуль силы упругости заменить на модуль F внешней деформирующей си­лы, уравновешивающей силу упругости.

Закон Гука.Многочисленные опыты показывают, что при малых дефор­мациях напряжение s прямо пропорционально относительно­му удлинению. Эта зависимость на­зывается законом Гука. Его можно записать так:

s = Е|e|. (1.4)

Относительное удлинение в формуле (1.4) взято по моду­лю, так как закон Гука справедлив как для деформации растя­жения, так и для деформации сжатия, когда e < 0.

Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости или модулем Юнга.

Если относительное удлинение e = 1, то s = Е. Следователь­но, модуль Юнга равен напряжению, возникающему в стержне при его относительном удлинении, равном единице. Так как 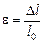, то при e = 1 Dl = l₀. А это значит, что модуль Юнга равен напряжению, возникающему в стержне при удвоении дли­ны образца. Практически любое тело (кроме резины) при упру­гой деформации не может удвоить свою длину: значительно раньше оно разорвется. Поэтому модуль Юнга определяют по формуле (1.4), измеряя напряжение s и относительное удли­нение e при малых деформациях.

Из формулы (1.4) видно, что единица модуля Юнга в СИ такая же, как и единица напряжения, т. е. паскаль.

Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l₀, S, F). Таким обра­зом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия. Модуль Юнга для некоторых металлов приведен в табл. 1.2.

Закон Гука, записанный в форме (1.4), легко привести к знакомому нам виду

F = k|Dl|. (1.5)

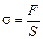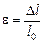Действительно, подставив в (1.4) и , получим 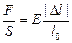. Откуда

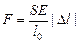. (1.6)

Обозначим

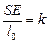, (1.7)

тогда

F = k|Dl|. (1.8)

Таким образом, согласно (1.7) жесткость k стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.

Т а б л и ц а 1.2