Параметры к задачам по формуле Бернулли
| № | k | l | m | m1 | m2 | n | n1 | n2 | N | p | q1 | q2 | r |
| 0.4846 | 0.4144 | 0.00721 | 0.4715 | ||||||||||
| 0.4399 | 0.6231 | 0.2895 | 0.2893 | ||||||||||
| 0.6059 | 0.004856 | 0.8595 | 0.1276 | ||||||||||
| 0.4011 | 0.3944 | 0.7075 | 0.1751 | ||||||||||
| 0.8426 | 0.3168 | 0.921 | 0.3976 | ||||||||||
| 0.6233 | 0.8535 | 0.09356 | 0.03515 | ||||||||||
| 0.05348 | 0.1977 | 0.0767 | 0.2954 | ||||||||||
| 0.8635 | 0.4691 | 0.3839 | 0.09883 | ||||||||||
| 0.3064 | 0.4332 | 0.5151 | 0.3222 | ||||||||||
| 0.02672 | 0.4188 | 0.1407 | 0.3021 | ||||||||||
| 0.3912 | 0.5804 | 0.07462 | 0.2207 | ||||||||||
| 0.03105 | 0.3374 | 0.9148 | 0.1983 | ||||||||||
| 0.8579 | 0.951 | 0.7553 | 0.2961 | ||||||||||
| 0.4019 | 0.4186 | 0.1017 | 0.4747 | ||||||||||
| 0.6116 | 0.7767 | 0.6779 | 0.1959 | ||||||||||
| 0.8754 | 0.1512 | 0.8242 | 0.09267 | ||||||||||
| 0.595 | 0.08735 | 0.2715 | 0.2872 | ||||||||||
| 0.7932 | 0.4718 | 0.8704 | 0.3137 | ||||||||||
| 0.5906 | 0.3328 | 0.9708 | 0.02482 | ||||||||||
| 0.5692 | 0.6145 | 0.2207 | 0.1301 | ||||||||||
| 0.6727 | 0.2807 | 0.2046 | 0.4477 | ||||||||||
| 0.01023 | 0.4391 | 0.1929 | 0.3642 | ||||||||||
| 0.3416 | 0.221 | 0.9568 | 0.1968 | ||||||||||
| 0.771 | 0.519 | 0.7388 | 0.4519 | ||||||||||
| 0.8698 | 0.007372 | 0.6798 | 0.1941 | ||||||||||
| 0.7256 | 0.7705 | 0.9213 | 0.1768 | ||||||||||
| 0.8939 | 0.9692 | 0.8443 | 0.3727 | ||||||||||
| 0.5356 | 0.904 | 0.1054 | 0.3697 | ||||||||||
| 0.7801 | 0.2227 | 0.9038 | 0.1001 | ||||||||||
| 0.1974 | 0.4785 | 0.8927 | 0.3402 | ||||||||||
| 0.7974 | 0.4144 | 0.9567 | 0.1839 | ||||||||||
| 0.8488 | 0.8416 | 0.3315 | 0.0547 | ||||||||||
| 0.6287 | 0.4275 | 0.8875 | 0.1015 | ||||||||||
| 0.6169 | 0.7349 | 0.4333 | 0.3274 | ||||||||||
| 0.2507 | 0.08175 | 0.2671 | 0.3438 | ||||||||||
| 0.7881 | 0.847 | 0.5279 | 0.03978 | ||||||||||
| 0.7139 | 0.3596 | 0.7941 | 0.01391 | ||||||||||
| 0.08151 | 0.0944 | 0.4867 | 0.1536 | ||||||||||
| 0.8553 | 0.1884 | 0.559 | 0.07134 | ||||||||||
| 0.3075 | 0.9134 | 0.3472 | 0.03393 | ||||||||||
| 0.473 | 0.3103 | 0.9112 | 0.3625 | ||||||||||
| 0.1919 | 0.3415 | 0.3685 | 0.347 | ||||||||||
| 0.995 | 0.2723 | 0.2113 | 0.3274 | ||||||||||
| 0.6476 | 0.1725 | 0.05017 | 0.04916 | ||||||||||
| 0.1741 | 0.06545 | 0.2488 | 0.02483 | ||||||||||
| 0.275 | 0.9637 | 0.1449 | 0.232 | ||||||||||
| 0.8389 | 0.4465 | 0.6081 | 0.3639 | ||||||||||
| 0.3712 | 0.1793 | 0.1969 | 0.34 | ||||||||||
| 0.2325 | 0.4721 | 0.7618 | 0.1861 | ||||||||||
| 0.2317 | 0.2486 | 0.6365 | 0.02499 | ||||||||||
| 0.971 | 0.2774 | 0.1744 | 0.08478 | ||||||||||
| 0.02291 | 0.8224 | 0.9632 | 0.1553 |
25 Асимптотические формулы для формулы Бернулли
При больших n вычисление по формуле Бернулли вероятности Рn (m) представляет собой трудную задачу.
Однако на практике такие задачи возникают довольно часто. Поэтому появляется потребность в выводе приближенных асимптотических формул, дающих возможность с высокой степенью точности вычислять как вероятность Рn(m), так и суммарные вероятности.
Обычно здесь рассматривают две ситуации:
1. “Редкие” события. Это ситуация, когда вероятность р появления события в каждом испытании сравнительно мала, то есть каждый успех - сравнительно редкое событие, а среднее число успехов np довольно значительно. В этом случае Рn(m) хорошо приближается распределением Пуассона .
2. Другая математическая модель ( теоремы Муавра-Лапласа ) дает довольно точное приближение в ситуации, когда вероятность успеха р и неуспеха q велики, то есть отделены от 0 и 1, а значит величина npq сравнительно велика
Сопоставим на конкретном примере условия, при которых применимы теоремы Муавра-Лапласа и Пуассона.
Представим себе сосуд V, содержащий разряженный газ, и выделим мысленно в этом сосуде какую-нибудь определенную часть - ячейку В. Допустим n молекул газа перемещаются в сосуде V свободно и независимо друг от друга так, что для любой определенной молекулы вероятность найти ее в ячейке В равна отношению р объемов В и V независимо от того, сколько других молекул уже находятся в ячейке.
Поставим прежде всего задачу определить ввероятность Рn(m) того, что в ячейке В будет ровно m молекул. Эта задача легко сводится к схеме Бернулли. Представим себе, что мы производим наблюдения за каждой из молекул с целью установить, находится ли молекула в ячейке В. Эти наблюдения состоят из n испытаний, при каждом из которых может произойти или не произойти событие, состоящее в том, что данная молекула находится в ячейке В. Вероятность этого события при каждом испытании будет равна р независимо от исхода остальных событий. Но тогда 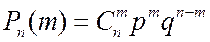 .
.
Будем увеличивать теперь число n молекул газа в V. Осуществим это увеличение массы газа двумя способами:
1. При постоянном давлении.
2. При постоянном объеме.
Рассмотрим оба случая отдельно.
Пусть масса газа увеличивается при постоянном давлении ( например, путем присоединения к сосуду новых и новых сосудов такого же объема ). В этом случае будет изменяться не только общее число молекул n, но и вероятность попадания молекул в ячейку В.
В самом деле эта вероятность равна отношению объема ячейки В к общему объему, заполняемому газом, а этот объем растет. Отсюда ясно, что в этом случае в обширном объеме разряженного газа для величины Рn (m) следует исследовать ситуацию 1 ( то есть применить теорему Пуассона ).
Отметим, что в этом случае нельзя реально увеличивать n до бесконечности, так как при увеличении объема наступает момент, когда уже нельзя будет считать попадание всех молекул в данную ячейку равновероятным. Но до наступления этого момента общее число молекул n, вообще говоря, будет уже достаточно велико, чтобы пользоваться предельной теоремой.
Пусть теперь масса газа увеличивается при постоянном объеме, то есть сосуд V остается неизменным. В этом случае картина распределения молекул с ростом их числа n не меняется, и вероятность того, что молекула находится в ячейке В равна р. Таким образом в этом случае выполняются условия ситуации 2 ( локальной теоремы Муавра-Лапласа).
Следует отметить, что реально невозможно увеличивать общее число молекул n в сосуде V до бесконечности, так как наступит момент, когда придется учитывать взаимодействие молекул и, следовательно, попадание молекул в данную ячейку нельзя считать независимым от других. Но до наступления этого момента молекул будет уже достаточно много, чтобы применить предельную теорему.
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,951000 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз используют формулу Пуассона
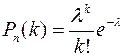 , (25.1)
, (25.1)
где λ=np=const – среднее число появлений события в n испытаниях.
Пример 25.1. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
N=1000, p=0,002, λ=np=2, k=3.
Искомая вероятность
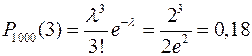 .
.
Пример 25.2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
n=500, p=0,004, λ=2.
По теореме сложения вероятностей
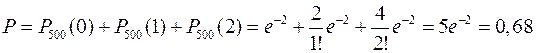 .
.
Пример 25.3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.
λ=np=1000·0,003=3
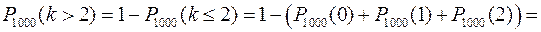
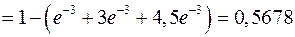 .
.
Пример 25.4. АТС производит в среднем n=3000 соединений в час, из них в среднем 3 соединения оказываются дефектными. Определить вероятность того, что в течение часа будет не более 6 дефектных соединений.
Решение: Искомая вероятность равна сумме: 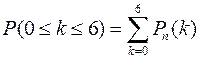 , где
, где 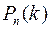 - вероятность того, что в течении часа произойдёт ровно k дефектов. Вероятность того, что некоторое соединение окажется дефектным, равна p=3/3000=0,001. Это малая величина, а число опытов велико. Можно вычислить
- вероятность того, что в течении часа произойдёт ровно k дефектов. Вероятность того, что некоторое соединение окажется дефектным, равна p=3/3000=0,001. Это малая величина, а число опытов велико. Можно вычислить 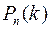 с помощью распределения Пуассона:
с помощью распределения Пуассона:
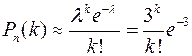
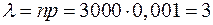
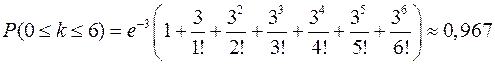
Пример 25.5. Срок службы для некоторого типа ламп составляет 1000 часов. Считая, что за этот срок лампа выходит из строя, определить число ламп, которые нужно заменить в течение одного часа при длительной эксплуатации радиоустройства, содержащего 2000 ламп. Найти вероятность выхода из строя за час одной, двух, трёх, 5 ламп, а также вероятность того, что за час ни одна лампа не выйдет из строя.
Решение. Число ламп, которые надо заменить 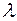 =2000/1000=2. Случайная величина Х – число ламп, вышедших из строя. По формуле Пуассона
=2000/1000=2. Случайная величина Х – число ламп, вышедших из строя. По формуле Пуассона 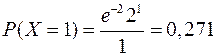
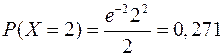
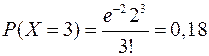
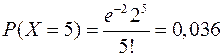
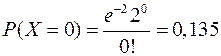
25.2 Локальная и интегральная формулыМуавра-Лапласа
Если n достаточно велико, p не сильно отличается от 0,5, имеет место формула Муавра-Лапласа, иногда называемая локальной формулойЛапласа.
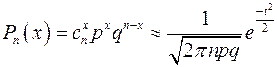 , где
, где 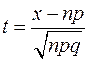 . (25.2)
. (25.2)
Из формулы видно, что одинаковые отклонения от величины np вправо и влево здесь имеют одинаковые вероятности. В формуле Бернулли это имеет место лишь при p=0.5.
Чтобы определить вероятность того, что в 50 испытаниях по схеме Бернулли при p=0.45 событие А наступило 30 раз, нужно воспользоваться таблицей значений функции 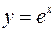 . Часто встречаются таблицы значений так называемой "локальной" функции Лапласа.
. Часто встречаются таблицы значений так называемой "локальной" функции Лапласа.
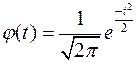 . (25.3)
. (25.3)
Если n достаточно велико, а p не сильно отличается от 0,5, имеет место интегральная формула Лапласа:
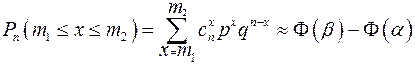 .
.
Здесь 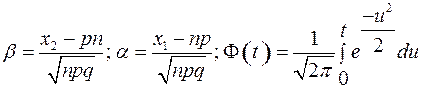 — функция Лапласа, значения которой определяются из таблиц.
— функция Лапласа, значения которой определяются из таблиц.
Для вычислений используются свойства функции Лапласа
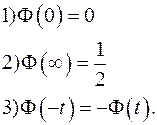
При t=3,5 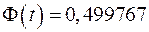 , и так как
, и так как 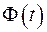 - монотонно возрастающая функция, в практических расчетах при
- монотонно возрастающая функция, в практических расчетах при 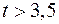 можно принимать
можно принимать 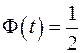 .
.
Пример 25.6. По данным ОТК завода, 0,8 всего объема выпускаемых микросхем не имеет дефектов. Найти вероятность того, что среди взятых наугад 400 микросхем дефекты будут иметь 80 микросхем.
Решение. В соответствии с формулой (25.2)
Pn(m)~ 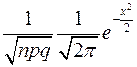 или Pn(m)~
или Pn(m)~ 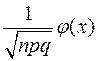 ,
,
где j(x) табулирована.
В условиях примера n=400, m=80, p=0,2, q=0,8. Отсюда
x= 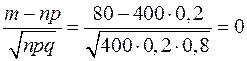 .
.
Из таблицы функций j(x) находим, что j(0)=0,3989.
Тогда искомая вероятность
P400(80)~ 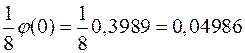 .
.
Заметим, что при вычислении этой вероятности по формуле Бернулли получается достаточно громоздкое выражение
P400(80)= 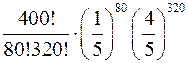 .
.
Пример 25.7. Игральную кость бросают 800 раз. Какова вероятность того, что число очков, кратное 3, выпадает не менее 280 и не более 294 раз?
Здесь 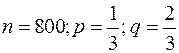
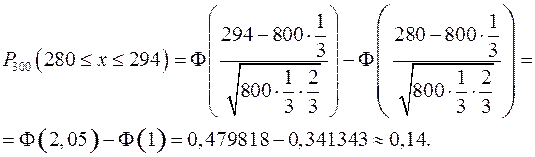
26 Условия задач типового расчета по теме предельные теоремы в схеме Бернулли
Задача N 1. Найти приближенное значение вероятности того, что число успехов S в схеме испытаний Бернулли с вероятностью успеха P, лежит в пределах a и b.
1. N= 60, P=0.39, a= 11, b= 12; 2. N= 80, P=0.24, a= 12, b= 17;
3. N=190, P=0.29, a= 59, b= 62; 4. N=340, P=0.10, a= 30, b= 42;
5. N=110, P=0.22, a= 18, b= 27; 6. N=760, P=0.17, a=129, b=148;
7. N=170, P=0.15, a= 18, b= 34; 8. N=400, P=0.80, a=310, b=349;
9. N=700, P=0.22, a=140, b=179; 10. N=120, P=0.48, a= 44, b= 62;
11. N=470, P=0.29, a=133, b=159; 12. N= 90, P=0.33, a= 40, b= 44;
13. N= 50, P=0.10, a= 1, b= 4; 14. N=750, P=0.17, a=114, b=139;
15. N=130, P=0.47, a= 55, b= 69; 16. N=200, P=0.26, a= 44, b= 55;
17. N=150, P=0.50, a= 56, b= 92; 18. N=730, P=0.23, a=132, b=188;
19. N=110, P=0.50, a= 41, b= 72; 20. N=180, P=0.12, a= 9, b= 24.
--------------------------------------------------------------------------
Задача N 2. В одном из экспериментов по моделированию на ЭВМ опытов с подбрасыванием правильной монеты из общего числа 'подбрасываний' N герб выпал M раз.
а) Какова априорная вероятность получить данный результат ?
б) Сколь вероятно при повторении эксперимента получить такое же или еще большее отклонение относительной частоты успехов от вероятности успеха в одном опыте ?
1. N=22948, M=11616; 2. N=17392, M= 8701;
3. N= 5641, M= 2847; 4. N= 6776, M= 3458;
5. N=13325, M= 6812; 6. N=23016, M=11531;
7. N=10437, M= 5258; 8. N=21788, M=10926;
9. N= 7755, M= 3976; 10. N=24925, M=12507;
11. N=21431, M=10734; 12. N=13843, M= 6933;
13. N= 6038, M= 3146; 14. N=13054, M= 6578;
15. N=20047, M=10062; 16. N=24728, M=12481;
17. N= 7190, M= 3612; 18. N=20214, M=10128;
19. N=22139, M=11153; 20. N=19482, M= 9766.
Задача N 3. В страховой компании застраховано N автомобилей. Вероятность поломки любого автомобиля в результате аварии равна P. Каждый владелец застрахованного автомобиля платит в год r рублей страховых и в случае поломки автомобиля в результате аварии получает от компании R рублей. Найти вероятность событий:
A={по истечении года работы страховая компания потерпит убыток},
B={страховая компания получит прибыль не менее M рублей}.
1. N=23000, P=0.013, r=11, R= 400, M=128000;
2. N= 5000, P=0.012, r=26, R= 900, M= 52000;
3. N=17000, P=0.010, r=19, R= 500, M= 98000;
4. N=22000, P=0.004, r=10, R= 900, M= 66000;
5. N=24000, P=0.001, r=28, R=1200, M= 28000;
6. N=18000, P=0.014, r=44, R= 900, M=197000;
7. N= 9000, P=0.015, r=29, R= 500, M= 74000;
8. N=13000, P=0.004, r=18, R= 300, M= 13000;
9. N=19000, P=0.010, r=41, R=1400, M=286000;
10. N=20000, P=0.015, r=13, R=1400, M=483000;
11. N= 5000, P=0.015, r=19, R=1300, M=105000;
12. N= 9000, P=0.013, r=17, R= 700, M= 93000;
13. N=16000, P=0.003, r=20, R= 800, M= 33000;
14. N=24000, P=0.007, r=20, R=1000, M=153000;
15. N=13000, P=0.006, r=26, R=1600, M=105000;
16. N= 9000, P=0.003, r=44, R= 600, M= 15000;
17. N=15000, P=0.007, r=10, R=1700, M=172000;
18. N=13000, P=0.011, r=13, R= 900, M=143000;
19. N=24000, P=0.012, r=21, R= 900, M=293000;
20. N= 9000, P=0.004, r= 9, R=1600, M= 64000;
Задача N 4. Дана вероятность успеха P. Каково должно быть значение N (число опытов), чтобы
с вероятностью a частота успеха S/N отличалась от P не более, чем на е.
1.P=0.26,a=0.09,e=0.031; 2.P=0.35,a=0.04,e=0.022;
3.P=0.64,a=0.25,e=0.066; 4.P=0.28,a=0.18,e=0.114;
5.P=0.45,a=0.22,e=0.085; 6.P=0.57,a=0.17,e=0.139;
7.P=0.35,a=0.02,e=0.135; 8.P=0.70,a=0.19,e=0.187;
9.P=0.42,a=0.36,e=0.188; 10.P=0.51,a=0.36,e=0.137; 11.P=0.31,a=0.06,e=0.012; 12.P=0.43,a=0.08,e=0.190;
13.P=0.73,a=0.28,e=0.125; 14.P=0.33,a=0.25,e=0.064; 15.P=0.47,a=0.08,e=0.146; 16.P=0.39,a=0.33,e=0.122;
17.P=0.49,a=0.36,e=0.157; 18.P=0.29,a=0.14,e=0.188; 19.P=0.37,a=0.34,e=0.015; 20.P=0.53,a=0.07,e=0.057.
Задача N 5. Большая партия изделий содержит b% брака. Каков должен быть объем N случайной выборки,чтобы вероятность встретить в ней хотя бы одно бракованное изделие была не меньше P.
1. b=7.60,P=0.90; 2. b=8.00,P=0.93; 3. b=4.40,P=0.82;
4. b=7.20,P=0.79; 5. b=7.60,P=0.95; 6. b=5.40,P=0.81;
7. b=0.40,P=0.78; 8. b=3.50,P=0.75; 9. b=3.80,P=0.86;
10. b=7.00,P=0.91; 11. b=1.90,P=0.81; 12. b=2.30,P=0.87;
13. b=0.60,P=0.98; 14. b=6.40,P=0.98; 15. b=8.60,P=0.79;
16. b=5.90,P=0.82; 17. b=8.00,P=0.95; 18. b=7.30,P=0.81;
19. b=4.80,P=0.81; 20. b=7.70,P=0.77.
Задача N 6. Пользуясь предельным свойством биномиального распределения (закон редких явлений) найти вероятность того, что в цель попадет:
а) ни одного снаряда;
б) один снаряд;
в) m снарядов,
если известно, что по цели производиться N выстрелов и вероятность попадания в цель при одном выстреле равна P.
1. N= 37,P=0.0201,m=2; 2. N= 18,P=0.0559,m=4;
3. N= 42,P=0.0379,m=4; 4. N= 11,P=0.0464,m=2;
5. N= 24,P=0.0181,m=6; 6. N= 19,P=0.0490,m=6;
7. N= 20,P=0.0154,m=2; 8. N= 15,P=0.0533,m=3;
9. N= 21,P=0.0156,m=6; 10. N= 55,P=0.0512,m=5;
11. N= 48,P=0.0108,m=3; 12. N= 52,P=0.0117,m=6;
13. N= 40,P=0.0375,m=6; 14. N= 50,P=0.0196,m=5;
15. N= 35,P=0.0383,m=6; 16. N= 53,P=0.0566,m=2;
17. N= 24,P=0.0142,m=2; 18. N= 59,P=0.0247,m=2;
19. N= 56,P=0.0213,m=4; 20. N= 27,P=0.0272,m=6.
Задача N 7. Предположим, что нормальная частота заболеваний определенной болезнью среди крупного рогатого скота составляет b%. Для проверки новой вакцины N животным делают прививки. Какова вероятность иметь K здоровых среди N подвергнувшихся прививкам?
1.N=19,K=16,b=14; 2.N=27,K=20,b=27; 3.N=24,K=16,b=15;
4.N=22,K=16,b=23; 5.N=23,K=18,b=19; 6.N=28,K=26,b=32;
7.N=15,K=15,b=25; 8.N=25,K=15,b=11; 9.N=19,K=17,b=17;
10.N=27,K=22,b=10; 11.N=25,K=18,b=20; 12.N=19,K=17,b=14;
13.N=19,K=16,b=25; 14.N=25,K=19,b=12; 15.N=18,K=16,b=26;
16.N=28,K=24,b=24; 17.N=23,K=17,b=20; 8.N=26,K=23,b=15; 19.N=22,K=18,b=19; 20.N=18,K=15,b=20.
Задача N 8. Для стрелка, выполняющего упражнения в тире, вероятность попасть в "яблочко" равна P. Спортсмен сделал N выстрелов. Найти вероятность следующих событий:
A={ровно одно попадание}, B={ровно два попадания}, C={хотя бы одно попадание}, D={не менее M попаданий}.
1. N=11, M= 4, p=0.23; 2. N=12, M= 5, p=0.28;
3. N=12, M= 3, p=0.32; 4. N= 8, M= 5, p=0.14;
5. N= 9, M= 5, p=0.18; 6. N= 7, M= 4, p=0.22;
7. N= 8, M= 3, p=0.20; 8. N= 7, M= 4, p=0.12;
9. N= 8, M= 5, p=0.14; 10. N= 5, M= 3, p=0.31;
11. N= 8, M= 4, p=0.32; 12. N= 9, M= 3, p=0.18;
13. N= 9, M= 5, p=0.22; 14. N= 5, M= 3, p=0.18;
15. N= 7, M= 4, p=0.26; 16. N= 5, M= 3, p=0.30;
17. N= 7, M= 4, p=0.14; 18. N=12, M= 4, p=0.25;
19. N=10, M= 6, p=0.13; 20. N= 7, M= 3, p=0.25.
Приложение. Справочные таблицы для расчётов
Дата добавления: 2016-04-11; просмотров: 2520;
