Параметры к задачам по геометрической вероятности
| № | a | d | k | m | n | N | r | № | a | d | k | m | n | N | r | |
9 Сложные события. Нахождение вероятностей сложных событий
В основе теоретико-множественного метода изложения теории вероятностей лежит предположение, что рассматриваемому стохастическому эксперименту всегда может быть поставлено в соответствие некоторое множество W, точки которого выражают наиболее полную информацию о возможных результатах в данном эксперименте.
Множество W называют пространством описаний элементарных случайных событий, а его точки – описаниями элементарных случайных событий (описаниями элементарных исходов), если это множество состоит из взаимоисключающих исходов эксперимента, а каждый интересующий нас результат эксперимента может быть однозначно описан с помощью элементов этого множества.
С множеством W связывают некоторую систему подмножеств 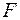 , обладающую определёнными свойствами, называемую алгеброй подмножеств множества W. Любое множество из
, обладающую определёнными свойствами, называемую алгеброй подмножеств множества W. Любое множество из 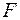 называется случайным событием.
называется случайным событием.
Раз событие формально есть подмножество множества W, то над событиями выполняются те же операции, что и над множествами.
Пусть для некоторого опыта выбрано пространство Ω элементарных событий.
Определение 9.1.Случайные события А и В в пространстве Ω называются эквивалентными или равными (обозначаются А=В), если они состоят из одних и тех же элементарных событий.
|
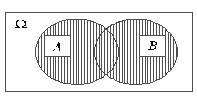
Определение 9.2.Суммой (объединением) двух событий А и В (обозначается А+В или A 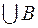 ) называется событие
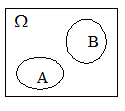
) называется событие 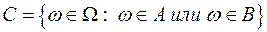 . Событие С означает, что в результате опыта появляется или событие А, или событие В, или оба события А и В вместе.
. Событие С означает, что в результате опыта появляется или событие А, или событие В, или оба события А и В вместе.
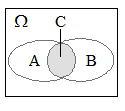 Определение 9.3.Произведением двух событий А и В (обозначается А.В,
Определение 9.3.Произведением двух событий А и В (обозначается А.В, 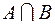 или АВ) называется событие
или АВ) называется событие 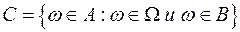 . Событие С означает, что в результате опыта событие А и событие В появляются одновременно.
. Событие С означает, что в результате опыта событие А и событие В появляются одновременно.
Определение 9.4.События А и В называются несовместными, если АВ=Æ, то есть если эти события не могут появиться в результате опыта одновременно.
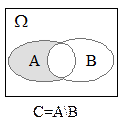
 Определение 9.5.Разностью событий А и В (обозначается А\В или А-В) называется событие
Определение 9.5.Разностью событий А и В (обозначается А\В или А-В) называется событие 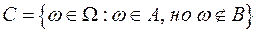 .
.
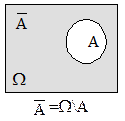
Определение 9.6.Событие Ω\А называется противоположным событию А и обозначается как 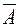 .
.
Теорема сложения. Для любых событий А и В
P(A+B)=P(A)+P(B)-P(AB).
Следствие 9.1. Если события А и В несовместимы, то
P(A+B)=P(A)+P(B).
Действительно, в этом случае АВ=Æ и Р(АВ)=0.
Следствие 9.7. Для любого события А
Р( 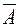 )=1-Р(А).
)=1-Р(А).
Это следует из равенства А+ 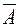 =Ω и следствия 1.
=Ω и следствия 1.
Определение 9.8. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Определение 9.9.События 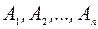 независимы в совокупности, если для любых k из них
независимы в совокупности, если для любых k из них 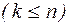 выполняется соотношение:
выполняется соотношение:
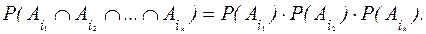
Если это соотношение выполняется лишь при k=2 , то события называются попарно независимыми. Попарной независимости n событий (n>2) недостаточно для независимости этих событий в совокупности.
Не следует путать понятия независимости и несовместности событий. Напомним, что события А и В в опыте несовместны, если они не могут наступать одновременно, то есть 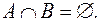
Определение 9.9. Вероятность события А, вычисленная при условии, что имело место событие В, называется условной вероятностью события А.
Если Р(В)>0, то условная вероятность 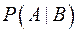 события А при условии, что произошло событие В вычисляется по формуле:
события А при условии, что произошло событие В вычисляется по формуле:
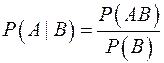 .
.
Из определения условной вероятности события следует:
Теорема умножения. Если Р(В)>0, то Р(АВ)=Р(В) 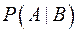 .
.
В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились, то есть:
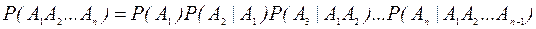 .
.
Вероятность произведения независимых событий равна произведению вероятностей этих событий: 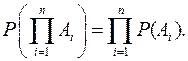
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.
Пусть события 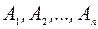 независимы в совокупности и
независимы в совокупности и 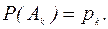 Найти вероятности событий:
Найти вероятности событий:
A ={не произойдет ни одного из событий 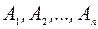 }; B = {произойдет хотя бы одно из событий
}; B = {произойдет хотя бы одно из событий 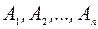 }.
}.
Решение: Если не произойдут события 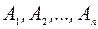 , это значит, что будут иметь место противоположные им события
, это значит, что будут иметь место противоположные им события 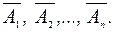 Следовательно,
Следовательно, 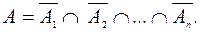 Воспользовавшись тем, что при независимости событий
Воспользовавшись тем, что при независимости событий 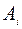 , события
, события 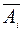 так же будут независимыми, получаем:
так же будут независимыми, получаем: 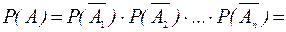
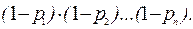 По определению операции объединения событий, событие В может быть представлено в виде:
По определению операции объединения событий, событие В может быть представлено в виде: 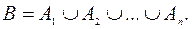 Для независимых событий легко вычисляется вероятность пересечения этих событий, поэтому здесь целесообразно воспользоваться законом де Моргана. В результате будем иметь:
Для независимых событий легко вычисляется вероятность пересечения этих событий, поэтому здесь целесообразно воспользоваться законом де Моргана. В результате будем иметь: 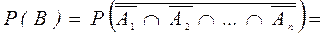
= 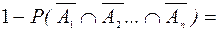
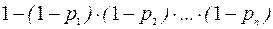 или
или
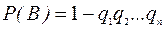 ,
,
где qi – вероятности противоположных событий 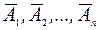 .
.
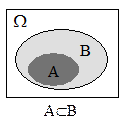
Определение 9.10.Говорят, что событие A влечет событие B ( обозначается AÌB), если при наступлении события A обязательно наступает и событие B.
Если событие A состоит в том, что наудачу брошенная точка попала в область A, а событие B - в область B, то соотношение AÌB выполняется тогда, когда область A целиком содержится в области B. Если AÌB и одновременно BÌA, то A=B. Очевидно, что для любого события A имеет место включение вида ÆÌAÌW.
Определение 9.11.Пусть W - множество взаимоисключающих исходов некоторого опыта и на этом множестве задана система подмножеств F, удовлетворяющая условиям:
1) WÎF, ÆÎF;
2) из того, что AÎF, следует, что также 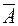 ÎF;
ÎF;
3) из того, что AÎF и BÎF, следует, что A 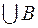 ÎF, A
ÎF, A 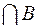 ÎF и A\BÎF.
ÎF и A\BÎF.
Тогда множество F называется алгеброй событий.
Если дополнительно к перечисленным условиям выполняется еще следующее условие:
4) из того, что AiÎF для i=1,2,..., следует, что 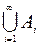 ÎF и
ÎF и 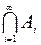 ÎF, то множество F называется s-алгеброй.
ÎF, то множество F называется s-алгеброй.
Элементы s-алгебры F, заданной на множестве W, называются наблюдаемыми случайными событиями.
Определение 9.12.Неэлементарное событие принадлежащее алгебре или s-алгебре событий называется сложным событием.
Под операциями над случайными событиями часто понимаются операции над соответствующими множествами. В результате можно составить таблицу соответствий между алгеброй множеств и алгеброй событий.
| Обозначения | Теория множеств | Теория вероятностей |
| w | Элемент множества, точка | Исход, элементарное событие |
| W | Множество точек, пространство | Пространство исходов (элементарных событий); достоверное событие |
| F | s-алгебра подмножеств | s-алгебра событий |
| AÎF | Множество точек | Событие (если wÎA, то говорят, что наступило событие A) |
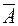 =W\A =W\A
| Дополнение множества A, то есть множество точек w, не входящих в A | Событие, состоящее в ненаступлении события A. |
A 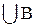
| Объединение множеств A и B, то есть множество точек w, входящих в A или в В | Событие, состоящее в том, что произошло событие A, либо событие B |
A 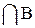 (или AB)
(или AB)
| Пересечение множеств A и B, то есть множество точек w, входящих в A и в B | Событие, состоящее в том, что одновременно произошло и событие A, и событие B |
| Æ | Пустое множество | Невозможное событие |
A 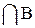 =Æ =Æ
| Множества A и B не пересекаются | События A и B несовместны (не могут наступать одновременно) |
| A+B | Сумма множеств, то есть объединение непересекающихся множеств | Событие, состоящее в том, что произошло одно из двух несовместных событий |
| A\B | Разность множеств A и B, то есть множество точек, входящих в A, но не входящих в B | Событие, состоящее в том, что произошло событие A, но не произошло событие B |
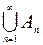
| Объединение множеств A1, A2,... | Событие, состоящее в наступлении хотя бы одного из событий A1,A2,... |
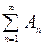
| Сумма,то есть объединение попарно непересекающихся множеств A1,A2,... | Событие, состоящее в наступлении одного из несовместных событий A1,A2,,,. |
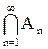
| Пересечение множеств A1,A2,... | Событие, состоящее в том, что одновременно произошли события A1,A2,,, |
| AÌB | A есть подмножество B | Событие A влечет событие B |
| A=B | Множества A и B равны | События A и B эквиваленты |
| Алгебра или s-алгебра множеств | Алгебра или s-алгебра событий |
Отправным пунктом аксиоматического определения вероятностей событий является рассмотренная выше алгебра и s-алгебра событий.
Аксиома 1. Каждому случайному событию A поставлено в соответствие неотрицательное число P(A), называемое его вероятностью.
Аксиома 2. P(W)=1.
Аксиома 3 (аксиома сложения). Если последовательность событий Аi такова, что Ai 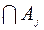 =Æ при i ¹ j, то
=Æ при i ¹ j, то
P( 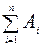 )=
)= 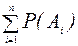 . (9.1)
. (9.1)
При рассмотрении различных вопросов в теории вероятностей часто приходится рассматривать последовательности случайных событий, поэтому возникает необходимость в дополнительном предположении, названном расширенной аксиомой сложения.
Расширенная аксиома сложения. Если событие A равносильно наступлению хотя бы одного из попарно несовместных событий A1,A2,...,An,..., то
P(A)=P(A1)+P(A2)+...+P(An)+... .
Расширенная аксиома сложения может быть заменена равносильной ей аксиомой непрерывности.
Аксиома непрерывности. Если последовательность событий B1,B2,...,Bn,... такова, что каждое последующее влечет за собой предыдущее и произведение всех событий Bnесть невозможное событие, то P(Bn)®0 при n®¥.
Для n совместных событий теорема сложения имеет вид
P( 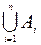 )=
)= 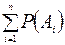 -
- 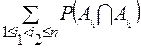 +
+ 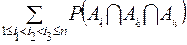 -...+
-...+
+(-1) 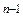 P(
P( 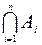 ). (9..2)
). (9..2)
Для несовместных событий имеем соотношение
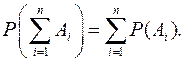
В общем случае P( 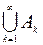 )£
)£ 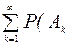 ).
).
10 Примеры задач по сложным событиям
Пример 10.1. Турист из пункта А в пункт В может попасть двумя дорогами. Обозначим события: Е1 - турист пошел первой дорогой, Е2 - турист пошел второй дорогой. Из пункта В в пункт С ведут три дороги. Обозначим события: D1 - турист пошел первой дорогой, D2 - турист пошел второй дорогой, D3 - турист пошел третьей дорогой. Если событие F1 - турист от пункта А до пункта В выбрал дорогу наугад, а от пункта В до пункта С пошел третьей дорогой, то F1=(E1+E2)D3. Если событие F2 - турист от пункта А до пункта В пошел не первой дорогой, а от пункта В до пункта С не третьей дорогой, то F2=E2(D1+D2). Если событие F3 - турист дошел от пункта А до пункта С, то F3=(E1+E2) (D1+D2+D3).
Пример 10. 2. Из первых десяти натуральных чисел наугад выбирают одно. Найти вероятность того, что выбранное число четное или кратное пяти.
Пусть событие А - выбранное число четное, событие В - выбранное число кратно пяти. Тогда событие А+В - выбранное число четное или кратно пяти, событие АВ - выбранное число четное и кратно пяти. По классическому определению вероятности Р(А)=0,5 Р(В)=0,2 и Р(АВ)=0,1. Следовательно, по теореме сложения Р(А+В)=0,5+0,2-0,1=0,6.
Заметим, что в этом простом опыте вероятность события А+В можно легко найти непосредственно по классическому определению вероятности, так как: А+В={2; 4; 5; 6; 8; 10} для пространства элементарных событий Ω ={1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
Пример 10. 3. В ящике содержатся 10 одинаковых по форме и весу шаров. Среди этих шаров 6 белых и 4 черных. Наугад вынимают последовательно два шара. Найти вероятность того, что вынутые шары белые.
Пусть событие А - первый вынутый шар белый; событие В -второй вынутый шар белый. По классическому определению вероятности Р(А)=0,6 Р(В/А)=5/9. Следовательно, Р(АВ)=Р(А)Р(В/А)=1/3.
Пример 10.4. Брошены 3 игральные кости. Найти вероятность выпадения хотя бы одной “шестерки” на верхних гранях костей.
Обозначим событие А - выпала хотя бы одна “шестерка”, тогда событие 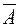 - не выпало ни одной “шестерки”. По теореме умножения
- не выпало ни одной “шестерки”. По теореме умножения
Р( 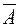 )=(5/6)3. Тогда Р(А)=1-Р(
)=(5/6)3. Тогда Р(А)=1-Р( 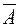 )=1-(5/6)3.
)=1-(5/6)3.
Пример 10. 5. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.
Пусть А – попадание первого стрелка, Р(А)=0,8;
В – попадание второго стрелка, Р(В)=0,9.
Тогда 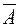 - промах первого,
- промах первого, 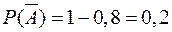 ;
;
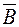 - промах второго,
- промах второго, 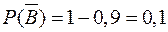 .
.
Найдем нужные вероятности.
а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.
б) 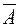
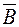 - двойной промах,
- двойной промах, 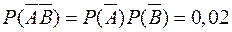 .
.
в) А+В – хотя бы одно попадание,
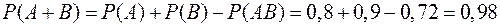 .
.
г) 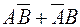 - одно попадание,
- одно попадание,
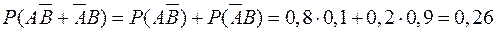 .
.
Пример 10. 6. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1. 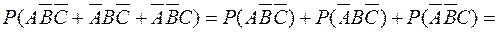
=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.
2. 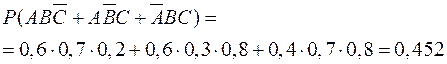 .
.
3. P(АВС)=0,6·0,7·0,8=0,336.
11 Условия задач расчета по теме сложные события
Задача №1. Два студента ищут нужную им книгу в букинистических магазинах. Вероятность того, что книга будет найдена первым студентом, равна n, а вторым -m. Какова вероятность, что только один из студентов найдёт книгу?
Задача №2. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна n; для второго и третьего стрелков эти вероятности соответственно равны m и k. Найти вероятность того, что только один из стрелков поразит цель.
Задача №3. Два спортсмена должны выполнить норму мастера спорта. Вероятность того, что первый спортсмен выполнит норму, равна n, а второй -m. Найти вероятность того, что норма будет выполнена только одним спортсменом.
Задача №4. Студент выучил "b" из "a" вопросов программы. Найти вероятность того, что студент не знает хотя бы один из предложенных ему трёх вопросов.
Задача №5. В партии среди "a" изделий "b" изделий являются первого сорта, а (a-b) второго. Наудачу одно за другим без возвращения в партию берут 3 изделия. Найти вероятность того, что хотя бы одно изделие окажется первого сорта.
Задача №6. В ящике лежит d белых и z красных одинаковых на ощупь шаров. Наудачу вынимают три шара. Какова вероятность того, что хотя бы один из них белый?
Дата добавления: 2016-04-11; просмотров: 1010;
