Параметры для задач по классической вероятности

6 Геометрические вероятности

Существуют эксперименты, исходы которых нельзя описать с помощью конечных пространств элементарных событий. В этих случаях иногда бывает полезным понятие геометрической вероятности.

Пусть между множествомW элементарных исходов случайного эксперимента и множеством S точек некоторой прямой или плоскости, или пространства, имеющим конечную меру m(S) можно установить взаимно-однозначное соответствие, а также можно установить взаимно-однозначное соответствие между множеством элементарных исходов, благоприятствующих событию А, и подмножеством s ÍS, имеющим конечную меру m(s). Под мерой множества понимается длина, площадь и объем соответственно.

Тогда вероятность Р(А) события А определяется равенством:

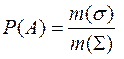(6.1)

и называется геометрической вероятностью. Формулу (6.1) часто записывают в виде

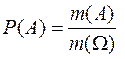, (6.2)

подразумевая отождествление А и Ωс sиS, соответственно.

Этот метод вычисления вероятности применяется тогда, когда по условиям эксперимента вероятность появления элементарного события (точки пространства Ω) во множестве А пропорциональна мере множества А и не зависит от его расположения в пространстве Ω. В таком случае говорят, что случайная точка имеет равномерное распределение в пространстве Ω.

Пример 6.1. На окружности единичного радиуса случайным образом появляются три точки А, В и С. Найти вероятность того, что треугольник АВС остроугольный.

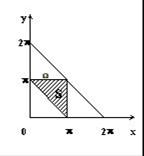Будем измерять длины дуг единичной окружности между точками в таком направлении, чтобы при движении по окружности за точкой А следовала точка В, а за точкой В - точка С. Обозначим через х - длину дуги АВ, через у - длину дуги ВС. Тогда различным исходам рассматриваемого эксперимента можно сопоставить точки плоскости ХОY с координатами х и у, удовлетворяющими неравенствам 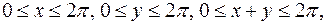то есть, 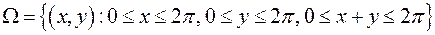. Если событие S - треугольник АВС остроугольный, то .

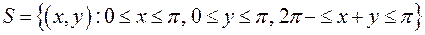Очевидно, площадь области W равна 2p ², а площадь области S равна 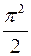. Следовательно, вероятность .

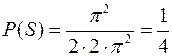Пример 6.2. Два человека обедают в столовой, которая открыта с 12 до 13 часов. Каждый из них приходит в произвольный момент времени и обедает в течение 10 минут. Какова вероятность их встречи?

Пусть x — время прихода первого в столовую, а y — время прихода второго .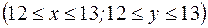

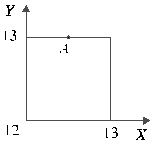
Можно установить взаимно-однозначное соответствие между всеми парами чисел (x;y) (или множеством исходов) и множеством точек квадрата со стороной, равной 1, на координатной плоскости, где начало координат соответствует числу 12 по оси X и по оси Y, как изображено на рисунке 6. Здесь, например, точка А соответствует исходу, заключающемуся в том, что первый пришел в 12.30, а второй - в 13.00. В этом случае, очевидно, встреча не состоялась.

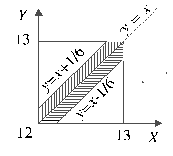
Если первый пришел не позже второго (y ³ x), то встреча произойдет при условии 0 £ y - x £ 1/6 (10 мин.- это 1/6 часа).

Если второй пришел не позже первого
(x ³ y), то встреча произойдет при условии
0 £ x - y £ 1/6..

Между множеством исходов, благоприятствующих встрече, и множеством точек области s, изображенной на рисунке в заштрихованном виде, можно установить взаимно-однозначное соответствие.

Искомая вероятность p равна отношению площади области s к площади всего квадрата.. Площадь квадрата равна единице, а площадь области s можно определить как разность единицы и суммарной площади двух треугольников, изображенных на. Отсюда следует:

.

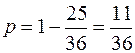7 Условия задач расчета по теме геометрические вероятности

Задача №1. На N-километровом участке линии электропередачи, соединяющей пункты А и D и проходящей через пункты В и С, произошел разрыв. Найти вероятность того, что разрыв произошел между пунктами В и С, если расстояние между пунктами А и В (измеренное вдоль линии электропередачи) равно "м" км, между пунктами С и D - "к" км.

Задача №2. Ученику, чтобы добраться от дома до школы необходимо часть пути проехать на трамвае, часть - на троллейбусе и часть - на автобусе. Интервалы движения трамваев, троллейбусов и автобусов соответственно равны "к" мин., "n" мин., "m" мин., Найти вероятность того, что ученик на пути в школу будет ожидать транспорт на остановках в сумме не более "d" минут.

Задача № 3. На бесконечную шахматную доску со стороной квадрата "а" наудачу бросается монета радиуса "r". Найти вероятности следующих событий:

А = (монета попадёт целиком внутрь одного квадрата),

В = (монета пересечёт не более одной стороны квадрата).