Параметры к задачам по теме сложные события
| № | a | b | d | z | n | m | k |
| 0.1723 | 0.8178 | 0.5374 | |||||
| 0.807 | 0.9654 | 0.7854 | |||||
| 0.04877 | 0.08798 | 0.2128 | |||||
| 0.6474 | 0.5769 | 0.2107 | |||||
| 0.4931 | 0.5927 | 0.5899 | |||||
| 0.09847 | 0.5805 | 0.6844 | |||||
| 0.6958 | 0.7886 | 0.4603 | |||||
| 0.2881 | 0.8816 | 0.3779 | |||||
| 0.1305 | 0.9679 | 0.8859 | |||||
| 0.2945 | 0.418 | 0.01994 | |||||
| 0.5386 | 0.3586 | 0.08334 | |||||
| 0.8333 | 0.3171 | 0.2855 | |||||
| 0.6388 | 0.7818 | 0.7491 | |||||
| 0.06461 | 0.06115 | 0.4448 | |||||
| 0.01318 | 0.3976 | 0.8278 | |||||
| 0.8977 | 0.4452 | 0.1014 | |||||
| 0.2747 | 0.5686 | 0.3761 | |||||
| 0.1215 | 0.6062 | 0.8961 | |||||
| 0.1685 | 0.3752 | 0.02718 | |||||
| 0.3395 | 0.9058 | 0.1065 | |||||
| 0.6096 | 0.8121 | 0.3062 | |||||
| 0.6369 | 0.9482 | 0.0184 | |||||
| 0.111 | 0.1971 | 0.7031 | |||||
| 0.6576 | 0.5139 | 0.6986 | |||||
| 0.2052 | 0.8251 | 0.5527 | |||||
| 0.1203 | 0.6906 | 0.04756 | |||||
| 0.411 | 0.3965 | 0.6279 | |||||
| 0.551 | 0.9828 | 0.2578 | |||||
| 0.5513 | 0.253 | 0.2971 | |||||
| 0.2599 | 0.6808 | 0.4588 | |||||
| 0.7719 | 0.9507 | 0.8502 | |||||
| 0.1416 | 0.2713 | 0.7752 | |||||
| 0.8666 | 0.2027 | 0.8457 | |||||
| 0.5259 | 0.1699 | 0.276 | |||||
| 0.06164 | 0.7221 | 0.3826 | |||||
| 0.3584 | 0.5568 | 0.5442 | |||||
| 0.661 | 0.9965 | 0.1491 | |||||
| 0.537 | 0.5982 | 0.04406 | |||||
| 0.5073 | 0.5252 | 0.4525 | |||||
| 0.1853 | 0.8326 | 0.0139 | |||||
| 0.1612 | 0.5511 | 0.4831 | |||||
| 0.2883 | 0.005369 | 0.7638 | |||||
| 0.7513 | 0.8175 | 0.3144 | |||||
| 0.7705 | 0.1309 | 0.1049 | |||||
| 0.3989 | 0.3816 | 0.4937 | |||||
| 0.04295 | 0.06526 | 0.6891 | |||||
| 0.2706 | 0.01618 | 0.8258 | |||||
| 0.1989 | 0.3698 | 0.1879 | |||||
| 0.2607 | 0.2301 | 0.4031 | |||||
| 0.785 | 0.7464 | 0.7867 | |||||
| 0.7585 | 0.4394 | 0.4848 | |||||
| 0.5267 | 0.827 | 0.2249 |
13 Формула полной вероятности
Пусть пространство элементарных событий Ω представлено в виде
Ω =Н1+Н2+Н3+...+Нn+..., где Нk- попарно несовместные события, которые часто называют гипотезами.
Если Р(Нk)>0 при k=1,2,..., то для любого события А справедлива формула полной вероятности
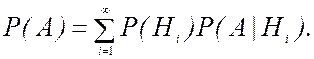
Здесь 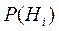 — вероятность
— вероятность 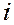 -ой гипотезы, а
-ой гипотезы, а 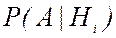 — условная вероятность события
— условная вероятность события 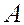 при осуществлении данной гипотезы.
при осуществлении данной гипотезы.
14 Примеры задач по формуле полной вероятности.
Пример 14.1. В первом ящике лежат 1 белый шар и 4 черных, а во втором ящике 1 белый и 7 черных. В первый ящик добавляются два шара, случайно выбранных из второго ящика. Найти вероятность того, что шар, выбранный наугад из пополненного первого ящика, будет черным.
Пусть А - событие, вероятность которого требуется найти. Рассмотрим события: Н1- в первый ящик добавили два черных шара; Н2 - в первый ящик добавили один белый и один черный шар. Тогда: 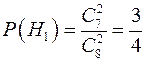 ,
, 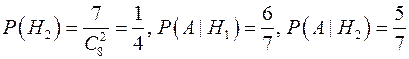 .Следовательно, по формуле полной вероятности
.Следовательно, по формуле полной вероятности 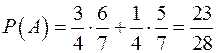 .
.
Пример 14.2. В первом ящике лежат 1 белый шар и 4 черных, а во втором ящике 1 белый и 7 черных. В первый ящик добавляются два шара, случайно выбранных из второго ящика. Найти вероятность того, что шар, выбранный наугад из пополненного первого ящика, будет черным.
Пусть А- событие, вероятность которого требуется найти. Рассмотрим события: Н1- в первый ящик добавили два черных шара; Н2 - в первый ящик добавили один белый и один черный шар. Тогда: 
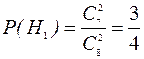 ,
, 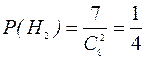 ,
, 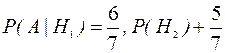 . Следовательно, по формуле полной вероятности
. Следовательно, по формуле полной вероятности 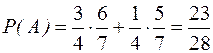 .
.
Пример 14. 3. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле р1=0,3, при втором р2=0,6, при третьем р3=0,8. При одном попадании вероятность поражения цели r1=0,4, при двух попаданиях r2=0,7, при трех попаданиях r3=1. Определить вероятность поражения цели при трех выстрелах.
Рассмотрим полную группу несовместных событий:
В1 – было одно попадание;
В2 – было два попадания;
В3 – было три попадания;
В4 – не было ни одного попадания.
Определим вероятность каждого события. По теоремам умножения и сложения вероятностей будем иметь
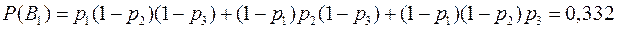 .
.
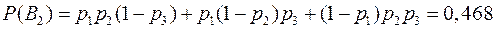 .
.
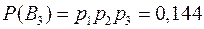 .
.
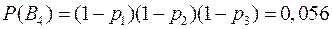 .
.
Пусть событие А – цель поражена. Выпишем условные вероятности поражения цели при осуществлении каждого из событий В1, В2, В3, и В4.
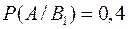 ,
, 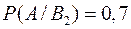 ,
, 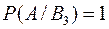 ,
, 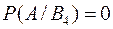 .
.
Тогда по формуле полной вероятности
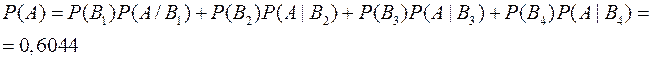
15 Условия задач типового расчета по теме формула полной вероятности
Задача №1. Радиолокационная станция ведёт наблюдение за объектом, который может применять или не применять помехи. Если объект не применяет помех, то за один цикл обзора станция обнаруживает его с вероятностью р0; если применяет - с вероятностью р1. Вероятность того, что во время цикла будут применены помехи, равна р и не зависит от того, как и когда применялись помехи в остальных циклах. Найти вероятность того, что объект будет обнаружен хотя бы один раз за n циклов обзора.
Задача №2. Завод изготовляет изделия, каждое из которых с вероятностью р имеет дефект. В цехе имеются три контролёра; изделие осматривается только одним контролёром, с одинаковой вероятностью первым, вторым или третьим. Вероятность обнаружения дефекта (если он имеется) для j-го контролёра равна qj (j=1,2,3 ). Если изделие не было забраковано в цехе, то оно попадёт в ОТК завода, где дефект, если он имеется, обнаруживается с вероятностью р0.
Определить вероятности следующих событий: А - изделие будет забраковано; В - изделие будет забраковано в цехе; С - изделие будет забраковано в ОТК завода.
Задача №3. Производится стрельба по цели одним снарядом. Цель состоит из трёх частей, площади которых равны S1,S2,S3 (S1+S2+S3=S). Для попавшего в цель снаряда вероятность попасть в ту или другую часть пропорциональна площади части. При попадании в первую часть цель поражается с вероятностью р1; во вторую часть - с вероятностью р2; в третью - р3. Найти вероятность поражения цели, если известно, что в неё попал один снаряд.
Задача №4. Имеется две партии однородных изделий; первая партия состоит из N изделий, среди которых n дефектных; вторая партия состоит из M изделий, среди которых m дефектных. Из первой партии берётся случайным образом K изделий, а из второй L изделий; эти K+L изделий смешиваются, и образуется новая партия. Из новой смешанной партии берётся наугад одно изделие. Найти вероятность того, что изделие будет дефектным.
Задача №5. Производится n независимых выстрелов зажигательными снарядами по резервуару с горючим. Каждый снаряд попадает в резервуар с вероятностью р. Если в резервуар попал один снаряд, горючее воспламеняется с вероятностью р1; если два снаряда - с полной достоверностью. Найти вероятность того, что при n выстрелах горючее воспламенится.
Дата добавления: 2016-04-11; просмотров: 1473;
