Параметры к задачам по формуле полной вероятности
| № | K | L | M | m | N | n | p | p0 | p1 | p2 | p3 |
| 0.5794 | 0.8967 | 0.1732 | 0.1224 | 0.4482 | |||||||
| 0.5651 | 0.6547 | 0.1156 | 0.8495 | 0.7387 | |||||||
| 0.528 | 0.7485 | 0.2949 | 0.6219 | 0.9002 | |||||||
| 0.9451 | 0.8521 | 0.1372 | 0.2122 | 0.1416 | |||||||
| 0.7937 | 0.8797 | 0.259 | 0.518 | 0.1722 | |||||||
| 0.2725 | 0.822 | 0.1431 | 0.3483 | 0.09872 | |||||||
| 0.0518 | 0.5898 | 0.2969 | 0.8291 | 0.6267 | |||||||
| 0.3415 | 0.4531 | 0.2351 | 0.9281 | 0.0735 | |||||||
| 0.8915 | 0.6226 | 0.2919 | 0.1298 | 0.2364 | |||||||
| 0.4355 | 0.6414 | 0.2735 | 0.01718 | 0.03408 | |||||||
| 0.6957 | 0.8553 | 0.2854 | 0.07229 | 0.6568 | |||||||
| 0.4969 | 0.6158 | 0.009076 | 0.02179 | 0.3637 | |||||||
| 0.4213 | 0.8596 | 0.2361 | 0.1366 | 0.6695 | |||||||
| 0.4013 | 0.6135 | 0.2908 | 0.6893 | 0.09291 | |||||||
| 0.3114 | 0.6004 | 0.1668 | 0.8905 | 0.5247 | |||||||
| 0.6152 | 0.7939 | 0.2596 | 0.6976 | 0.2362 | |||||||
| 0.07029 | 0.7879 | 0.182 | 0.5406 | 0.2158 | |||||||
| 0.02068 | 0.5325 | 0.2871 | 0.8628 | 0.5124 | |||||||
| 0.5324 | 0.6489 | 0.2927 | 0.05504 | 0.2168 | |||||||
| 0.187 | 0.4858 | 0.1689 | 0.4982 | 0.2315 | |||||||
| 0.3566 | 0.6322 | 0.1309 | 0.6407 | 0.7138 | |||||||
| 0.8707 | 0.5665 | 0.232 | 0.9542 | 0.6289 | |||||||
| 0.7779 | 0.8145 | 0.2892 | 0.8543 | 0.8624 | |||||||
| 0.02509 | 0.7212 | 0.2647 | 0.8713 | 0.4283 | |||||||
| 0.9455 | 0.5221 | 0.2691 | 0.1301 | 0.1005 | |||||||
| 0.102 | 0.65 | 0.03019 | 0.1776 | 0.9134 | |||||||
| 0.8819 | 0.4337 | 0.1736 | 0.004222 | 0.0506 | |||||||
| 0.9241 | 0.8595 | 0.1712 | 0.361 | 0.2919 | |||||||
| 0.5907 | 0.681 | 0.2274 | 0.8185 | 0.03989 | |||||||
| 0.9121 | 0.689 | 0.06664 | 0.04857 | 0.6311 | |||||||
| 0.347 | 0.7112 | 0.159 | 0.183 | 0.7715 | |||||||
| 0.9459 | 0.7015 | 0.1483 | 0.4238 | 0.1467 | |||||||
| 0.7007 | 0.4284 | 0.03004 | 0.9804 | 0.1771 | |||||||
| 0.6424 | 0.5787 | 0.1386 | 0.5128 | 0.1272 | |||||||
| 0.2232 | 0.8786 | 0.04562 | 0.1919 | 0.9824 | |||||||
| 0.3297 | 0.4128 | 0.1171 | 0.8707 | 0.2736 | |||||||
| 0.5304 | 0.4943 | 0.02968 | 0.3272 | 0.0171 | |||||||
| 0.5011 | 0.5331 | 0.076 | 0.7003 | 0.7367 | |||||||
| 0.6119 | 0.6647 | 0.0005952 | 0.7394 | 0.7996 | |||||||
| 0.02746 | 0.7605 | 0.07408 | 0.9329 | 0.6328 | |||||||
| 0.9976 | 0.6461 | 0.1307 | 0.6052 | 0.429 | |||||||
| 0.9113 | 0.7284 | 0.2483 | 0.3041 | 0.3195 | |||||||
| 0.7947 | 0.5792 | 0.02446 | 0.8528 | 0.3146 | |||||||
| 0.8635 | 0.6621 | 0.09193 | 0.9539 | 0.2116 | |||||||
| 0.1239 | 0.628 | 0.0996 | 0.8182 | 0.7746 | |||||||
| 0.4827 | 0.7572 | 0.1598 | 0.5844 | 0.4208 | |||||||
| 0.9877 | 0.5076 | 0.2055 | 0.9118 | 0.03545 | |||||||
| 0.3201 | 0.5464 | 0.2085 | 0.7051 | 0.997 | |||||||
| 0.1017 | 0.4132 | 0.06318 | 0.07501 | 0.6624 | |||||||
| 0.6101 | 0.8968 | 0.2321 | 0.9971 | 0.05609 | |||||||
| 0.7199 | 0.6202 | 0.2616 | 0.3099 | 0.9533 | |||||||
| 0.9477 | 0.5275 | 0.2027 | 0.328 | 0.5729 |
| № | q1 | q2 | q3 | S1 | S2 | S3 |
| 0.006124 | 0.6947 | 0.6415 | ||||
| 0.3887 | 0.3126 | 0.5505 | ||||
| 0.7051 | 0.5002 | 0.6921 | ||||
| 0.6499 | 0.601 | 0.1559 | ||||
| 0.1767 | 0.1472 | 0.00115 | ||||
| 0.4291 | 0.1422 | 0.2615 | ||||
| 0.003287 | 0.8031 | 0.9991 | ||||
| 0.2588 | 0.9945 | 0.8619 | ||||
| 0.6214 | 0.9585 | 0.7341 | ||||
| 0.8798 | 0.2646 | 0.2799 | ||||
| 0.986 | 0.8059 | 0.1004 | ||||
| 0.4606 | 0.7692 | 0.4654 | ||||
| 0.7898 | 0.4414 | 0.7783 | ||||
| 0.8258 | 0.09614 | 0.7108 | ||||
| 0.7707 | 0.6693 | 0.9192 | ||||
| 0.4756 | 0.09811 | 0.06292 | ||||
| 0.1397 | 0.6916 | 0.1054 | ||||
| 0.678 | 0.3486 | 0.2138 | ||||
| 0.6569 | 0.4638 | 0.6173 | ||||
| 0.4141 | 0.5923 | 0.1512 | ||||
| 0.3915 | 0.9976 | 0.5374 | ||||
| 0.4583 | 0.7207 | 0.3503 | ||||
| 0.6929 | 0.3923 | 0.7245 | ||||
| 0.3744 | 0.3047 | 0.7872 | ||||
| 0.4068 | 0.8761 | 0.1878 | ||||
| 0.7096 | 0.2146 | 0.5565 | ||||
| 0.8669 | 0.638 | 0.8924 | ||||
| 0.1656 | 0.3595 | 0.3732 | ||||
| 0.6923 | 0.7322 | 0.5282 | ||||
| 0.03118 | 0.07715 | 0.7407 | ||||
| 0.9238 | 0.8365 | 0.2729 | ||||
| 0.6546 | 0.2054 | 0.06673 | ||||
| 0.5287 | 0.1443 | 0.07977 | ||||
| 0.2388 | 0.3664 | 0.5063 | ||||
| 0.8062 | 0.1741 | 0.5227 | ||||
| 0.7396 | 0.4951 | 0.8162 | ||||
| 0.7246 | 0.7747 | 0.7292 | ||||
| 0.1496 | 0.1429 | 0.9992 | ||||
| 0.721 | 0.1102 | 0.4318 | ||||
| 0.947 | 0.5886 | 0.02094 | ||||
| 0.9957 | 0.9041 | 0.6707 | ||||
| 0.9926 | 0.2862 | 0.3806 | ||||
| 0.831 | 0.7246 | 0.1774 | ||||
| 0.6546 | 0.6828 | 0.816 | ||||
| 0.9681 | 0.5923 | 0.972 | ||||
| 0.4438 | 0.9362 | 0.9246 | ||||
| 0.5708 | 0.691 | 0.2033 | ||||
| 0.9391 | 0.5648 | 0.9825 | ||||
| 0.8081 | 0.4634 | 0.766 | ||||
| 0.2861 | 0.5597 | 0.7409 | ||||
| 0.5886 | 0.8736 | 0.7231 | ||||
| 0.04854 | 0.9913 | 0.4832 |
17 Формула Байеса
Пусть пространство элементарных событий Ω представлено в виде:
Ω =Н1+Н2+Н3+...+Нn+..., где Нk- попарно несовместные события, которые часто называют гипотезами.
Если Р(Нk)>0 при k=1,2,..., то для любого события А справедлива формула Байеса 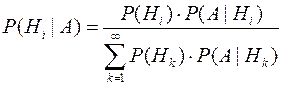 , где i=1,2,...
, где i=1,2,...
18 Примеры задач по формуле Байеса
Пример 18.1. В турслете участвуют 70% девятиклассников и 30% десятиклассников. Среди девятиклассников 60% мальчиков, а среди десятиклассников 40% мальчиков. Все мальчики по очереди дежурят у костра, сменяясь каждый день. Найти вероятность того, что в случайно выбранный день у костра дежурит девятиклассник.
Пусть событие А - у костра дежурит мальчик, событие Н1 - у костра дежурит кто-то из девятиклассников; событие Н2 - у костра дежурит кто-то из десятиклассников. Тогда Р(Н1)=0,7; Р(Н2)=0,3; Р(А|Н1)=0,6; Р(А|Н2)=0,4.
Следовательно, по формуле Байеса
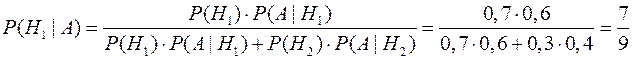 .
.
Пример 18.2. Страховая компания разделяет застрахованных по трем классам риска: 1 класс – малый риск, 2 класс – средний, 3 класс – большой риск. Среди всех клиентов компании 50% - первого класса риска, 30% - второго и 20% - третьего. Вероятность наступления страхового случая для первого класса риска равна 0.01, второго – 0.03, третьего – 0.08. Какова вероятность того, что клиент, получивший денежное вознаграждение за период страхования, относится к группе малого риска?
Решение. Пусть событие А означает, что клиент компании получил вознаграждение. Понятно, что событие А может наступить лишь совместно с одним из трех попарно несовместных событий: 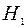 - клиент относится к первому классу риска;
- клиент относится к первому классу риска; 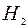 - клиент относится ко второму классу риска;
- клиент относится ко второму классу риска; 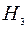 - клиент относится к третьему классу риска. Необходимо определить условную вероятность
- клиент относится к третьему классу риска. Необходимо определить условную вероятность 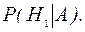 Из условия задачи известны вероятности гипотез:
Из условия задачи известны вероятности гипотез: 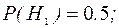
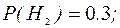
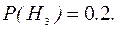 Известны также условные вероятности:
Известны также условные вероятности: 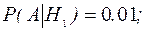
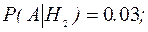
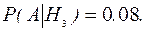 Искомую вероятность вычисляем по формуле Байеса, то есть
Искомую вероятность вычисляем по формуле Байеса, то есть
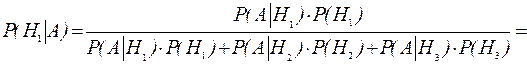
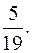
Пример 18.3. В канцелярии работают 4 секретарши, которые отправляют 40,10,30 и 20% исходящих документов. Вероятности неверной адресации документов секретаршами равны 0,01; 0,04; 0,06; 0,01 соответственно. Найти вероятность того, что документ, неверно адресованный, отправлен третьей секретаршей.
Решение. Введем гипотезы Hi- документ отправила i-я секретарша, i=1,2,3,4. Тогда по условию задачи P(H1)=0,4; P(H2)=0,1; H(Р3)=0,3; P(H4)=0,2. Обозначим через A событие, состоящее в том, что документ адресован неверно. Тогда по условию P(A|H1)=0,01; P(A|H2)=0,04; P(A|H3)=0,06; P(A|H4)=0,01 и искомая вероятность
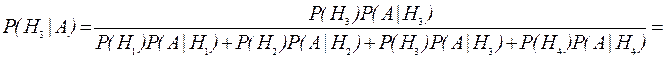 = 0,391.
= 0,391.
Пример 18. 4.30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.
Событие А – безотказная работа прибора;
В1 – прибор собран специалистом высокой квалификации;
В2 – прибор собран специалистом средней квалификации.
Выпишем вероятности гипотез: 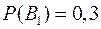 ,
, 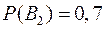 .
.
Условные вероятности события А: 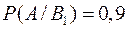 ,
, 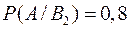 .
.
Вероятность события А: 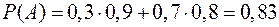 .
.
Определим вероятность гипотезы В1 при условии, что событие А произошло
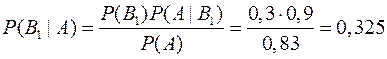 .
.
19 Условия задач типового расчета по теме формула Байеса
Задача № 1. Прибор состоит из двух узлов: работа каждого узла, безусловно, необходима для работы прибора в целом. Надёжность (вероятность безотказной работы в течение времени t) первого узла равна p1, второго p2. Прибор испытывался в течение времени t, в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.
Задача №2. Рассматривается посадка самолёта на аэродром. Если позволяет погода, лётчик сажает самолёт, наблюдая за аэродромом визуально. В этом случае вероятность благополучной посадки равна p1. Если аэродром затянут низкой облачностью, лётчик сажает самолёт в слепую по приборам. Надёжность (вероятность безотказной работы) приборов слепой посадки равна P. Если приборы слепой посадки сработали нормально, то самолёт садится благополучно с той же вероятностью p1, что и при визуальной посадке. Если же приборы слепой посадки не сработали, то лётчик может благополучно посадить самолёт только с очень малой вероятностью p2. Известно, что самолёт приземлился благополучно. Найти вероятность того, что лётчик пользовался приборами слепой посадки, если известно, что в k% всех случаев посадки аэродром затянут низкой облачностью.
Задача № 3. Пассажир может обратиться за получением билета в одну из трёх касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно p1, p2, p3. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равна для первой кассы P1, для второй P2, для третьей P3. Пассажир направился за билетом в одну из касс и приобрёл билет. Найти вероятность того, что это была первая касса.
Задача № 4. Производится один выстрел по плоскости, на которой расположены две цели : 1 и 2. Вероятность попадания в цель 1 равна p1, в цель 2 равна p2. После выстрела получено известие, что попадание в цель 1 не произошло. Какова теперь вероятность того, что произошло попадание в цель 2?
Дата добавления: 2016-04-11; просмотров: 3379;
