Параметры к задачам по формуле Байеса
| № | k | P | p1 | p11 | p2 | p3 | px1 | px2 | px3 |
| 0.9911 | 0.1055 | 0.931 | 0.06828 | 0.8622 | 0.799 | 0.6683 | 0.5994 | ||
| 0.9368 | 0.143 | 0.9342 | 0.982 | 0.04762 | 0.8344 | 0.7207 | 0.5995 | ||
| 0.9211 | 0.1212 | 0.9272 | 0.6155 | 0.05618 | 0.7699 | 0.7788 | 0.5996 | ||
| 0.905 | 0.008288 | 0.9172 | 0.3675 | 0.08501 | 0.8529 | 0.6471 | 0.5997 | ||
| 0.9249 | 0.1791 | 0.9065 | 0.8601 | 0.9625 | 0.7001 | 0.7063 | 0.5998 | ||
| 0.9145 | 0.1297 | 0.9964 | 0.2419 | 0.8786 | 0.8496 | 0.7136 | 0.5999 | ||
| 0.9608 | 0.1149 | 0.9446 | 0.05099 | 0.4031 | 0.8588 | 0.7022 | 0.6000 | ||
| 0.9197 | 0.00303 | 0.9179 | 0.1725 | 0.6585 | 0.8448 | 0.7942 | 0.6001 | ||
| 0.9762 | 0.2596 | 0.9472 | 0.2201 | 0.9452 | 0.8077 | 0.7405 | 0.6002 | ||
| 0.9636 | 0.2099 | 0.9249 | 0.7869 | 0.002247 | 0.7204 | 0.6207 | 0.6003 | ||
| 0.9174 | 0.1807 | 0.9277 | 0.08369 | 0.04946 | 0.7193 | 0.6933 | 0.6004 | ||
| 0.9963 | 0.1679 | 0.9822 | 0.1365 | 0.422 | 0.7324 | 0.6098 | 0.6005 | ||
| 0.9198 | 0.1135 | 0.963 | 0.5626 | 0.6039 | 0.8342 | 0.6233 | 0.6006 | ||
| 0.9047 | 0.2812 | 0.9007 | 0.6323 | 0.4144 | 0.8776 | 0.748 | 0.6007 | ||
| 0.9036 | 0.2892 | 0.929 | 0.4537 | 0.6231 | 0.8139 | 0.6009 | 0.6008 | ||
| 0.9082 | 0.1752 | 0.9859 | 0.3338 | 0.004856 | 0.7223 | 0.7913 | 0.6009 | ||
| 0.9569 | 0.1221 | 0.9707 | 0.2825 | 0.3944 | 0.8467 | 0.7502 | 0.6010 | ||
| 0.9219 | 0.1496 | 0.9921 | 0.8732 | 0.3168 | 0.7976 | 0.7357 | 0.6011 | ||
| 0.9305 | 0.2624 | 0.9094 | 0.8685 | 0.8535 | 0.8602 | 0.7326 | 0.6012 | ||
| 0.9411 | 0.2345 | 0.9077 | 0.7954 | 0.1977 | 0.7697 | 0.6142 | 0.6013 | ||
| 0.9252 | 0.1765 | 0.9384 | 0.635 | 0.4691 | 0.8997 | 0.7723 | 0.6014 | ||
| 0.9509 | 0.08379 | 0.9515 | 0.5948 | 0.4332 | 0.8896 | 0.7778 | 0.6015 | ||
| 0.9988 | 0.2623 | 0.9141 | 0.1943 | 0.4188 | 0.8261 | 0.6304 | 0.6016 | ||
| 0.9122 | 0.09042 | 0.9075 | 0.2315 | 0.5804 | 0.7291 | 0.7148 | 0.6017 | ||
| 0.9707 | 0.26 | 0.9915 | 0.2391 | 0.3374 | 0.7916 | 0.6351 | 0.6018 | ||
| 0.9295 | 0.05722 | 0.9755 | 0.4068 | 0.951 | 0.7097 | 0.7669 | 0.6019 | ||
| 0.9525 | 0.2671 | 0.9102 | 0.2725 | 0.4186 | 0.8485 | 0.7717 | 0.6020 | ||
| 0.9517 | 0.008643 | 0.9678 | 0.3794 | 0.7767 | 0.8301 | 0.7966 | 0.6021 | ||
| 0.9829 | 0.01778 | 0.9824 | 0.2065 | 0.1512 | 0.7469 | 0.7417 | 0.6022 | ||
| 0.9104 | 0.07708 | 0.9271 | 0.6046 | 0.08735 | 0.8989 | 0.7632 | 0.6023 | ||
| 0.9947 | 0.03484 | 0.987 | 0.3613 | 0.4718 | 0.8787 | 0.7948 | 0.6024 | ||
| 0.9474 | 0.1485 | 0.9971 | 0.976 | 0.3328 | 0.8784 | 0.6628 | 0.6025 | ||
| 0.9919 | 0.01479 | 0.9221 | 0.8958 | 0.6145 | 0.8232 | 0.6411 | 0.6026 | ||
| 0.9365 | 0.1013 | 0.9205 | 0.9535 | 0.2807 | 0.8462 | 0.7896 | 0.6027 | ||
| 0.966 | 0.1547 | 0.9193 | 0.2017 | 0.4391 | 0.8512 | 0.65 | 0.6028 | ||
| 0.9507 | 0.1237 | 0.9957 | 0.3555 | 0.221 | 0.7809 | 0.7732 | 0.6029 | ||
| 0.928 | 0.1803 | 0.9739 | 0.291 | 0.519 | 0.8434 | 0.6411 | 0.6030 | ||
| 0.9791 | 0.1427 | 0.968 | 0.09961 | 0.007372 | 0.8772 | 0.7507 | 0.6031 | ||
| 0.9858 | 0.2854 | 0.9921 | 0.7093 | 0.7705 | 0.779 | 0.6749 | 0.6032 | ||
| 0.9464 | 0.2505 | 0.9844 | 0.6719 | 0.9692 | 0.7976 | 0.7261 | 0.6033 | ||
| 0.9442 | 0.2405 | 0.9105 | 0.005783 | 0.904 | 0.8524 | 0.7473 | 0.6034 | ||
| 0.9379 | 0.261 | 0.9904 | 0.6046 | 0.2227 | 0.7671 | 0.6777 | 0.6035 | ||
| 0.9558 | 0.2817 | 0.9893 | 0.2906 | 0.4785 | 0.7721 | 0.796 | 0.6036 | ||
| 0.9837 | 0.283 | 0.9957 | 0.7469 | 0.4144 | 0.7163 | 0.6655 | 0.6037 | ||
| 0.901 | 0.03829 | 0.9331 | 0.9122 | 0.8416 | 0.8994 | 0.7255 | 0.6038 | ||
| 0.9041 | 0.1419 | 0.9888 | 0.6059 | 0.4275 | 0.7793 | 0.698 | 0.6039 | ||
| 0.9256 | 0.008002 | 0.9433 | 0.7842 | 0.7349 | 0.783 | 0.6537 | 0.6040 | ||
| 0.9708 | 0.1364 | 0.9267 | 0.5426 | 0.08175 | 0.7539 | 0.613 | 0.6041 | ||
| 0.9133 | 0.04083 | 0.9528 | 0.3947 | 0.847 | 0.745 | 0.6908 | 0.6042 | ||
| 0.9857 | 0.06384 | 0.9794 | 0.1019 | 0.3596 | 0.8284 | 0.7293 | 0.6043 | ||
| 0.9218 | 0.2392 | 0.9487 | 0.02746 | 0.0944 | 0.8758 | 0.6532 | 0.6044 | ||
| 0.9313 | 0.1975 | 0.9559 | 0.2589 | 0.1884 | 0.7823 | 0.725 | 0.6045 | ||
| 0.9607 | 0.2344 | 0.9347 | 0.2286 | 0.9134 | 0.8929 | 0.6205 | 0.6046 |
21 Испытания Бернулли. Формула Бернулли
Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.
Обычно эти два исхода называются “успехом” (У) или “неудачей” (Н) и соответствующие вероятности обозначают p и q. Ясно, что p³ 0, q³ 0 и p+q=1.
Пространство элементарных событий каждого испытания состоит из двух событий У и Н.
Пространство элементарных событий n испытаний Бернулли Ω содержит 2n элементарных событий, представляющих собой последовательности (цепочки) из n символов У и Н. Каждое элементарное событие является одним из возможных исходов последовательности n испытаний Бернулли. Поскольку испытания независимы, то, по теореме умножения, вероятности перемножаются, то есть вероятность любой конкретной последовательности - есть произведение, полученное при замене символов У и Н на p и q соответственно, то есть, например: Р(w )={У У Н У Н ... Н У }=p p q p q ... q q p .
Отметим, исход испытания Бернулли часто обозначают 1 и 0, и тогда элементарное событие в последовательности n испытаний Бернулли - есть цепочка, состоящая из нолей и единиц. Например: w =(1, 0, 0, ... , 1, 1, 0).
Испытания Бернулли представляют собой важнейшую схему, рассматриваемую в теории вероятностей. Эта схема названа в честь швейцарского математика Я. Бернулли (1654-1705), в своих работах глубоко исследовавших эту модель.
Основная задача, которая нас будет здесь интересовать: какова вероятность того события, что в n испытаниях Бернулли произошло m успехов?
При выполнении указанных условий вероятность того, что при проведении 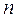 независимых испытаний событие
независимых испытаний событие 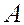 будет наблюдаться ровно m раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
будет наблюдаться ровно m раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
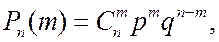 (21.1)
(21.1)
где 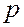 — вероятность появления
— вероятность появления 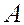 в каждом испытании, а
в каждом испытании, а 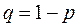 — вероятность того, что в данном опыте событие
— вероятность того, что в данном опыте событие 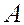 не произошло.
не произошло.
Если рассматривать Pn(m) как функцию m, то она задает распределение вероятностей, которое называется биномиальным. Исследуем эту зависимость Pn(m) от m, 0£m£n.
События Bm (m = 0, 1, ..., n), состоящие в различном числе появлений события А в n испытаниях, несовместны и образуют полную группу. Следовательно, 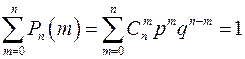 .
.
Рассмотрим соотношение:
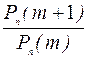 =
= 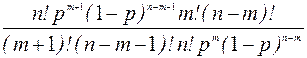 =
= 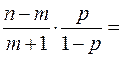
= 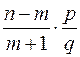 .
.
Отсюда следует, что Pn(m+1)>Pn(m), если (n-m)p>(m+1)q, т.е. функция Pn(m) возрастает, если m<np-q. Аналогично, Pn(m+1)<Pn(m), если (n-m)p<(m+1)q, т.е. Pn(m) убывает, если m>np-q.
Таким образом, существует число m0,при котором Pn(m) достигает наибольшего значения. Найдем m0.
По смыслу числа m0 имеем Pn(m0)³Pn(m0-1) и Pn(m0) ³Pn(m0+1), отсюда
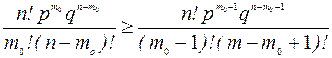 , (21.2)
, (21.2)
и
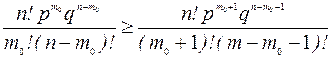 . (21.3)
. (21.3)
Решая неравенства (21.2) и (21.3) относительно m0, получаем:
p/m0³ q/(n-m0+1) Þ m0£np+p,
q/(n-m0) ³ p/(m0+1) Þ m0³np-q.
Итак, искомое число m0 удовлетворяет неравенствам
np-q£ m0£np+p. (21.4)
Так как p+q=1, то длина интервала, определяемого неравенством (21.4), равна единице и имеется, по крайней мере, одно целое число m0, удовлетворяющее неравенствам (21.4):
1) если np - q - целое число, то существуют два значения m0, а именно:
m0 = np - q и m0= np - q + 1 = np + p;
2) если np - q - дробное, то существует одно число m0, а именно единственное целое, заключенное между дробными числами, полученными из неравенства (21.4);
3) если np - целое число, то существует одно число m0, а именно m0 = np.
Число m0называется наиболее вероятным или наивероятнейшим значением (числом) появления события A в серии из n независимых испытаний.
22 Примеры испытаний Бернулли и формулы Бернулли
Пример 22.1. Наиболее известным примером испытаний Бернулли является последовательное бросание правильной симметричной монеты; здесь p=q=1/2. Если отказаться от условия симметричности монеты, то мы по-прежнему считаем последовательные испытания независимыми и вновь получаем испытания Бернулли, в которых вероятность успеха может быть произвольной.
Пример 22.2. В примере бросания правильной кости испытание Бернулли возникает, если мы будем описывать результат как А и не А (например, “успех” - если выпала цифра 6 и “неудача” в противном случае). Здесь p=1/6, q=5/6.
Если кость несимметрична, то соответствующие вероятности p и q могут измениться.
Пример 22.3. Стрелок совершает пять выстрелов по мишени, причем все выстрелы производятся практически в одних и тех же условиях. При этом попадание в яблоко мишени рассматривается как “успех” испытания, и число успехов за 5 испытаний может меняться от 0 до 5.
Пример 22.4. Из урны, содержащей N шаров, среди которых М - белых и N-M - черных, последовательно извлекается шар, фиксируется его цвет, и затем шар возвращается обратно. Ясно, что каждое такое извлечение есть испытание Бернулли с 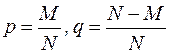 .
.
Пример 22.5 (проверка сывороток или вакцин). Предположим, что нормальная частота заболеваний определенной болезнью среди крупного рогатого скота составляет 25%. Для проверки новой вакцины n животным делают прививки. Разберем вопрос об оценке результата эксперимента.
Если вакцина абсолютно недейственна, вероятность иметь ровно k здоровых среди n подвергнувшихся прививкам Рn(k) ( в этом случае вероятность успеха р есть вероятность того, что животное здорово, и равно 0,75 ).
Для k=n=10, P10(10)=p10=0,7510 »0,056.
Для k=n=12, P12(12) » 0,032.
Таким образом, отсутствие заболеваний среди десяти или двенадцати животных можно рассматривать как подтверждение эффективности вакцины.
Пример 22.6. Имеется партия изделий. Каждое из изделий партии независимо от других может оказаться дефектным с вероятностью р. Из партии произвольным образом выбираются 15 изделий и эти изделия проверяются на годность. Если число дефектных изделий в выборке не более двух, то партию принимают, в противном случае - подвергают сплошному контролю. Какова вероятность того, что партия, для которой р=0,2 , будет принята ?
Решение. Искомая вероятность P- есть вероятность не более 2 успехов в 15 испытаниях схемы Бернулли с р=0,2.
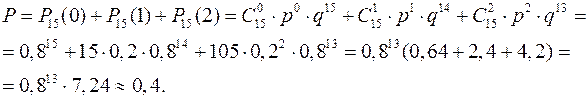
Пример 22.7. Для данного баскетболиста вероятность забросить мяч в корзину при броске - 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.
Решение. np-q £ m0 £ (n+1)p; 3,6 £ m0 £ 4,4; m0=4.
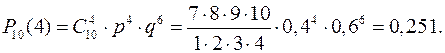
Пример 22.7.Известно, что 1/45 часть продукции, изготовляемой заводом, не удовлетворяет требованиям стандарта. Завод изготовил 4500 единиц продукции. Найти наивероятнейшее число изделий завода, удовлетворяющих требованиям стандарта.
Решение. Поскольку вероятность изготовления бракованного изделия q=1/45, то вероятность изделия, удовлетворяющего стандарту, p=44/45. По формуле (21.4)
450044/45-1/45 £ mo£ 450044/45+44/45,
или
4400-1/45 £ mo£ 4400+44/45.
Итак, искомое наиболее вероятное число изделий, удовлетворяющих требованиям стандарта, равна 4400.
Дата добавления: 2016-04-11; просмотров: 851;
