Опыт, явление, событие

Определение 1.1. Опытом (испытанием, экспериментом, наблюдением) называется реальная или мысленная реализация определенного комплекса условий и действий.

Результаты опыта можно охарактеризовать качественно и количественно.

Качественная характеристика опыта называется событием или явлением, если событие несёт в себе некоторую глобальность.

Определение 1.2. Событие называется случайным, если при осуществлении определённой совокупности условий S, то есть опыта, оно может либо произойти, либо не произойти.

Случайным (стохастическим) экспериментом будем называть эксперимент, в котором имеются случайные события и в основном рассматриваются и изучаются случайные события.

В дальнейшем, вместо того чтобы говорить “совокупность условий S осуществлена”, будем говорить кратко: ”произведено испытание (опыт)”. Таким образом, событие будет рассматриваться как результат испытания.

Случайный эксперимент (испытание, опыт) и случайные события этого опыта называются массовыми, если он может воспроизводиться реально или мысленно неограниченное число раз.

Теория вероятностей возникла как наука из убеждения, что в основе массовых случайных событий лежат детерминированные закономерности. Теория вероятностей изучает данные закономерности.

Например: определить однозначно результат выпадения "орла" или "решки" в результате подбрасывания монеты нельзя, но при многократном подбрасывании выпадает примерно одинаковое число "орлов" и "решек".

Определение 1.3. Элементарными событиями (исходами) будем называть такие результаты, которые удовлетворяют следующим условиям:

1) никакие два (или больше) исхода не происходят одновременно и, хотя бы один исход w происходит обязательно;

2) каково бы ни было событие А из рассматриваемого множества событий, по элементарному исходу w можно определить, произошло А или нет.

Совокупность Ω всех исходов опыта называют пространством элементарных событий.

Не всегда бывает легко выделить и описать пространство Ω элементарных событий.

Для различных стохастических экспериментов, желательно построить множество W и выяснить:

как случайному событию 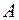, связанному с данным экспериментом, ставится в соответствие подмножество пространства описаний элементарных исходов W,

какая взаимосвязь результатов операций над случайными событиями и результатов соответствующих операций над подмножествами пространства W.

В зависимости оттого, что интересует нас в данном опыте, можно по-разному выбирать и описывать пространство элементарных событий.

Пример 1.1. Одновременно бросают три разные монеты. Если нас интересует, как выпадает каждая монета (кверху гербом или цифрой), то целесообразно рассмотреть пространство элементарных событий Ω₁ ={ГГГ, ЦГГ, ГЦГ, ГГЦ, ЦЦГ, ГЦЦ, ЦГЦ, ЦЦЦ}, где, например, элементарное событие ЦГГ означает, что первая монета выпала кверху цифрой, а вторая и третья - гербом. В другом случае, если нас интересует только число выпавших гербов, то имеет смысл рассматривать пространство элементарных событий Ω₂ = { 0, 1, 2, 3 } , в котором каждый элемент равен числу выпавших гербов. Если же важно знать, как упали монеты одинаково ( то есть все гербом кверху или цифрой кверху ) или нет, то достаточно рассмотреть, например, пространство элементарных событий Ω₃ = { + , - }, где “+” означает, что все монеты упали одинаково, а “-” - различно.

Пример 1. 2. Рассмотрим тот же опыт, что и в примере 1. Если событие А₁ - вторая монета упала гербом кверху, то в пространстве элементарных событий Ω₁ А₁ = { ГГГ, ЦГГ, ГГЦ, ЦГЦ }, а в пространстве Ω₂ А₂ = { 1, 2, 3 }.

Если же событие А₂ - выпал только один герб, то в пространстве Ω₁

А₂ = { ЦЦГ, ГЦЦ, ЦГЦ }, а в пространстве Ω₂ А₂ = { 1 }.
По отношению к Ω₃ характеризовать события А₁, А₂ становится затруднительным, поэтому при описании (рассмотрении) пространства Ω элементарных событий должно учитываться множество всех рассматриваемых событий.

Пример 1. 3. Каждый из четырех студентов, проживающих в одной комнате общежития, может присутствовать или не присутствовать на лекции по теории вероятностей. Рассматриваются события:

A -на лекции присутствует ровно один из четырех студентов;

B-на лекции присутствует хотя бы один из четырёх студентов;

C-на лекции присутствуют не менее двух из четырех студентов;

D-на лекции присутствуют ровно два из четырех студентов;

E-на лекции присутствуют ровно три из четырех студентов;

F-на лекции присутствуют все четыре студента.

Начнём с построения пространства элементарных исходов (элементарных событий) рассматриваемого эксперимента. Вспомним, что таким пространством называется любое множество W взаимоисключающих исходов эксперимента такое, что каждый интересующий нас результат эксперимента может быть однозначно описан с помощью элементов этого множества. В данном случае случайный эксперимент заключается в наблюдении за четырьмя студентами и выяснении, посещают ли они лекции по теории вероятностей. Нас интересует только количество студентов, присутствующих на лекции. Пусть элемент 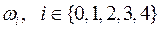описывает элементарный исход, означающий, что на лекции присутствовало ровно i студентов. Тогда 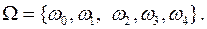Все случайные события формально есть подмножества множества описаний элементарных исходов. Выпишем формально все события, о которых идет речь в условии задачи. Для этого нужно перечислить описания элементарных исходов, благоприятствующих каждому из этих событий, то есть обеспечивающих появление этих событий. Таким образом, будем иметь:

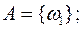
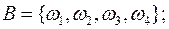
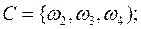
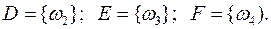
2 Классическая вероятность. Вероятности событий в опытах с конечным числом исходов

Любое случайное событие А, которое может произойти в опыте, может рассматриваться как подмножество из элементарных событий некоторого пространства Ω элементарных событий. Само пространство Ω отождествляется с любым событием, которое всегда наступает в опыте и называется достоверным. Пустое подмножество пространства Ω отождествляется с любым событием, которое никогда не наступает в рассматриваемом опыте. Это событие называется невозможным и обозначается символом Æ.

Вероятностьюсобытия А называется математическая оценка возможности появления этого события в результате опыта или вероятность случайного события 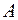- это численная мера степени объективной возможности наступления этого события.

Существует несколько методов определения вероятностей событий.

Пусть Ω = { w₁; w₂ ; ... w_n } - некоторое пространство элементарных событий соответствующих какому-то эксперименту. Каждому элементу w_i из Ω поставим в соответствие неотрицательное число p_i так, что p₁+p₂+...+p_n=1. Выбор чисел p_i происходит, как правило, исходя из сравнения возможностей различных исходов эксперимента. Число p_i называется вероятностью элементарного события w_i . Вероятностью любого события А называют число Р(А), равное сумме вероятностей элементарных событий, составляющих А. При этом, если событие А не содержит элементов, то вероятность Р( А ) = 0.

Пример 2.1 Из карточек разрезной азбуки составлено слово “математика”. Затем из карточек наугад выбирается одна. Рассмотрим пространство элементарных событий Ω= {а ; м ; т ; е ; к ; и }, где, например, элемент “и” означает, что выбрана карточка с буквой “и”. Обозначим через P(w) вероятность элементарного события w. Тогда целесообразно определить вероятности элементарных событий в этом опыте следующим образом: P(a)=0.3, P(м)=P(т)=0.2, P(е)=P(к)=P(и)=0.1. Действительно, возможность выбрать карточку с буквой “а” в три раза превышает возможность выбрать карточку с буквой “е”. Очевидно, P(а)+P(м)+P(т)+P(е)+P(к)+P(и)=1. Тогда, если событие А - выбрана карточка с гласной буквой, то вероятность Р(А)=P(а)+P(е)+P(и)=0.3+0.1+0.1=0.5.

Предположим, что по условиям опыта все элементарные события равновозможные, то есть каждое элементарное событие не имеет никаких преимуществ в появлении по сравнению с остальными элементарными событиями (то есть при большом количестве опытов все исходы наблюдаются с одинаковой частотой). Тогда имеет смысл считать, что р(w₁)=р(w₂)=...=р(w_n) и, следовательно, р(w_i )= .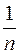

Обозначим через 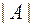- число элементов конечного множества А. Если событие А содержит k элементарных событий, то

P(А)=. 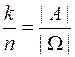. (2.1)

Исходы, при которых происходит некоторое событие 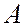называются благоприятными или благоприятствующими событию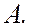

Тогда вероятность события 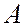по формуле (2.1) определяется как отношение числа благоприятных исходов к числу всех возможных.

Это определение вероятности события называется классическим.

Пример 2.2. Игральной костью называют выполненный из однородного материала кубик, грани которого помечены номерами 1; 2; 3; 4; 5; 6 так, что сумма чисел на противоположных гранях равна семи.

Игральная кость подбрасывается один раз. Пространство элементарных событий Ω = { 1; 2; 3; 4; 5; 6 } , где, например, элементарное событие 1 означает, что кость упала гранью с номером 1 вверху. Описание опыта позволяет считать все элементарные события в пространстве Ω равновозможными из-за симметричности игральной кости. Поэтому целесообразно полагать равными вероятности всех элементарных событий, то есть P(1)=P(2)=...=P(6)= .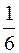

Пусть событие А - на верхней грани игральной кости выпал четный номер. Тогда А={2; 4; 6 } и Р(А)= 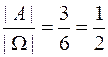. Пусть событие В - на верхней грани игральной кости выпало простое число. Тогда В={1; 2; 3; 5} и Р(В)= .

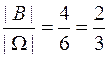Для вычисления вероятности по классическому определению необходимо находить число элементов в пространстве элементарных событий Ω и в различных случайных событиях - подмножествах A . Это часто удается сделать, используя комбинаторные методы. Большинство комбинаторных задач решается с помощью следующих двух основных принципов.

Принцип умножения. Если множество А содержит n элементов, а множество В содержит k элементов, то множество всех различных упорядоченных пар вида (a;b), где 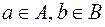содержит n×k элементов.

Пример 2.3. Из города К в город L можно попасть через город F и G, не соединенные между собой дорогой. Пусть из города К в город F ведут 4 разные дороги, из города F в город L ведут 2 разные дороги, из города К в город G ведут 2 разные дороги и из города G в город L ведут 3 разные дороги.

Каким числом различных путей можно совершить путешествие из города К в город L через города F и G ?

По принципу умножения число различных путей из города К в город L через город F равно 4^. 2=8, а число различных путей из города К в город L через город G равно 2^. 3=6. Следовательно, число различных путей из города К в город L через города F или G по принципу сложения равно 8+6=14.

Принцип сложения. Если множество С можно разбить на два непересекающихся подмножества А и В, множество А содержит n элементов, множество В содержит k элементов, то множество 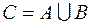содержит n+k элементов.

Множество, состоящее из n элементов, будем называть упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число (номер элемента) от 1 до n. Упорядоченные множества считаются различными, если они отличаются друг от друга либо некоторыми элементами, либо их порядком, то есть номерами. При этом элемент с меньшим номером называется предшествующим элементу с большим номером.

Упорядоченные k-элементные подмножества из n элементов называются размещениями из n элементов по k. Число различных размещений из n элементов по k обозначается 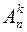. Используя принцип умножения легко показать, что

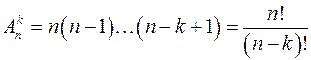, где n!=1^.2^. ... ^.n, (0!=1).

Пример 2.4. Сколько трехзначных чисел можно составить из цифр 1; 2; 3; 4; 5 так, чтобы ни одна из цифр не повторялась более одного раза?

Каждое трехзначное число указанного вида является размещением трех цифр из пяти данных в вопросе. Поэтому количество таких чисел равно .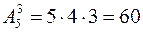

Размещения из n элементов по n называется перестановками множества из n элементов. Число всех различных перестановок множества из n элементов обозначается через 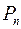. Очевидно, .

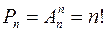Пример 2.5. Сколькими способами можно поставить на полке пять томов “Математической энциклопедии” ?

Каждой расстановке пяти книг на полке соответствует перестановка пяти чисел 1, 2, 3, ..., 5, поэтому существует 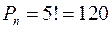способов расстановки 5 томов “Математической энциклопедии”.

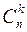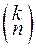Любое k-элементное подмножество множества из n элементов называется сочетанием из n элементов по k. В отличие от размещений сочетания являются неупорядоченными подмножествами и поэтому различаются только своими элементами. Число всех различных сочетаний из n элементов по k обозначается через или . Любое размещение из n элементов по k можно получить двумя последовательными действиями : а) - выбор сочетания из n элементов по k; в) - расстановка k элементов выбранного сочетания в определенном порядке. Очевидно, число всех различных размещений из n элементов по k равно ,

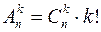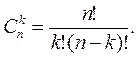
В частности, если имеется множество из 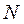объектов двух видов ( 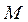элементов первого вида и 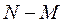— второго), из которых требуется выбрать 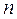элементов, среди которых должно быть 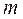предметов первого типа и 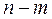второго, то число всех различных выборок такого вида равно: .

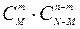Пример 2.6 Сколькими способами можно выбрать из 30 учеников класса 6 дежурных?

При выборе группы дежурных играет роль только состав группы и не играет роли порядок выбора, поэтому 6 дежурных можно выбрать способами .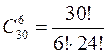

3 Примеры задач по классической вероятности.

Пример 3.1. В урне 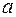белых и 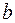черных шаров 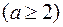. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми.

Решение. Для того, чтобы описать пространство элементарных исходов данного эксперимента, пронумеруем все шары. Пусть белые шары имеют номера от 1 до 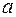, а черные – номера от 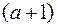до 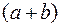. Множество 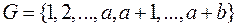означает множество всех шаров. Случайный эксперимент заключается в случайном выборе двух элементов из множества G. Тогда элементарный исход эксперимента может быть описан как множество из двух элементов, то есть 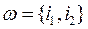, где 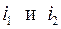- номера вынутых шаров. Заметим, что порядок выбора элементов 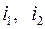здесь не важен. Все элементарные исходы равновозможные в силу симметрии эксперимента, их общее число равно 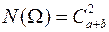. Запишем событие А, означающее, что выбраны два белых шара , A= 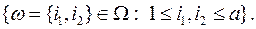Число элементарных исходов, благоприятствующих наступлению события А, равно 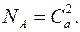Вероятность события А вычисляется как отношение числа элементарных исходов, благоприятствующих наступлению события А к общему числу элементарных исходов, то есть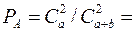

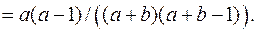
Пример 3.2. Игральный кубик подбросили два раза. Найти вероятность того, что сумма выпавших очков равна 5.

Решение. В данном случайном эксперименте случайно количество очков, выпавших на кубике при каждом броске. Поэтому элементарный исход такого случайного эксперимента может быть описан как арифметический вектор с двумя компонентами, где первая и вторая компоненты означают соответственно количество очков, выпавших при первом и втором броске игрального кубика. Все такие исходы будут равновозможными в силу симметрии случайного эксперимента.

Множество 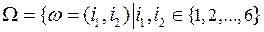всех элементарных исходов содержит 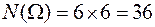различных элементов. Событие А формально запишется следующим образом: 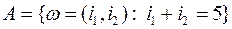. Для вычисления N(A) можно просто перебрать все описания элементарных исходов, содержащиеся в множестве А, а именно 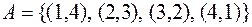, и 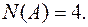Ответ: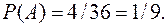

Замечание. Следует заметить, что если описывать элементарные исходы как неупорядоченные двухэлементные множества, то есть 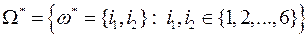, то интересующее нас случайное событие можно описать с помощью элементов множества 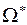, но в данном случае нельзя использовать классический способ определения вероятностей случайного события, так как элементарные исходы, описания которых содержатся в множестве 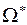, не являются равновозможными. Покажем это, используя равновозможность исходов, описания которых составляют множество .

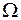Рассмотрим два различных элементарных исхода, которым соответствуют элементы 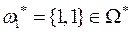и 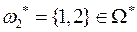. Для наступления элементарного случайного события { 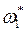} необходимо и достаточно появление элементарного исхода, описанного элементом 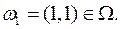Событию { 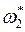}, соответствуют описания 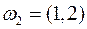и 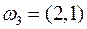. Таким образом событиям { 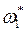} и { 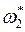} соответствует разное количество равновозможных элементарных случайных событий, описанных элементами множества 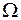, следовательно такие случайные события не являются одинаково вероятными.

Пример 3.3. В ящике 3 белых и 4 черных шара одинаковой формы и веса. Из ящика наугад выбирают три шара сразу. Найти вероятность того, что два шара из выбранных будут черными, а один - белый.

В качестве пространства элементарных событий W в описанном эксперименте можно рассматривать множество всевозможных троек шаров из семи шаров ящика. Тогда количество элементов пространства W равно 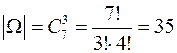. Пусть событие А - из трех выбранных шаров два - черные, а один - белый. Число способов выбора двух черных шаров из четырех черных шаров, имеющихся в ящике, равно 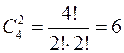. Число способов выбора одного белого шара из трех белых шаров, имеющихся в ящике, очевидно, равно 3. Поэтому по принципу умножения количество элементов события А равно | A |=6^.3=18. Следовательно, по классическому определению вероятности .

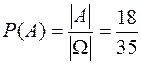4 Условия задач типового расчета по теме классическая вероятность

Задача №1. В магазин поступило N новых цветных телевизоров, среди которых M имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?

Задача №2. Из партии, содержащей N изделий, среди которых M бракованных, наудачу извлекают Z изделий для контроля. Найти вероятности следующих событий:

А=(в полученной выборке ровно К изделий бракованных);

В=( в полученной выборке нет ни одного бракованного изделия).

Задача №3. Множество Е состоит из N первых букв русского алфавита. Опыт состоит в выборе без возвращения М букв и записи слова в порядке поступления букв. Сколько М буквенных слов может быть получено в данном опыте? Какова вероятность того, что наудачу составленное слово будет оканчиваться буквой а?

Задача №4. Батарея из M орудий ведёт огонь по группе, состоящей из N целей. Орудия выбирают себе цели последовательно, случайным образом, при условии, что никакие два орудия стрелять по одной цели не могут. Найти вероятность того, что будут обстреляны цели с номерами 1,2,...,M.

Задача №5. В урне, а белых и b чёрных шаров. Из урны вынимают сразу пять шаров. Найти вероятность p того, что два из них будут белыми, а три чёрными.

Задача №6. В технической библиотеке имеются книги по математике, физике, химии и т.д., всего по n разделам науки. Поступили очередные m заказов на литературу. Считая, что любой состав заказанной литературы равновозможен, найти вероятности следующих событий:

а) заказаны книги из различных разделов науки;

б) заказаны книги из одного и того же раздела науки.

Задача № 7. Колоду из N красных и R чёрных карт разделили на две части, содержащих N и R карт соответственно. Найти вероятность события: все чёрные карты находятся в большей части.