Числовые характеристики случайных величин
1. Математическое ожидание – характеристика центра группирования случайных величин:
– для дискретных случайных величин
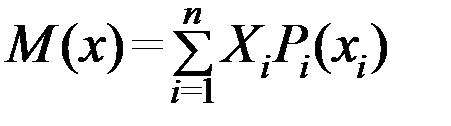 ; (2.27)
; (2.27)
– для непрерывных случайных величин
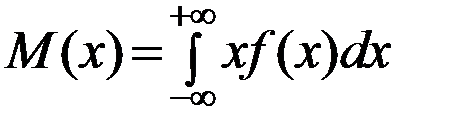 . (2.28)
. (2.28)
2. Модой непрерывной случайной величины называется то её значение,
в котором плотность вероятности наибольшая (т. М на рис. 2.4), М является точкой перегиба кривой.Модойдискретной случайной величины называется ее наиболее вероятное значение.
3. Медианой случайной величины Х называется такое её значение, для которого ограниченная кривой распределения площадь делится пополам (т. Ме на рис. 2.4). Площади справа и слева от медианы равны.Можно также определить медиану случайной величины X как такое ее значение Me, для которого
P(X < Me) = P(X > Me). В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
4. Значение случайной величины, соответствующее заданной вероятности, называется квантилью. Квантиль при вероятности, равной 0,5, называется медианой.
5. Дисперсия есть сумма произведений квадратов разностей случайных величин и математических ожиданий:
– для дискретных случайных величин
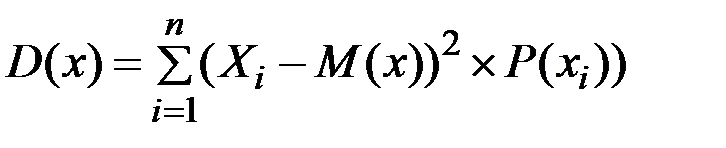 ; (2.29)
; (2.29)
– для непрерывных случайных величин:
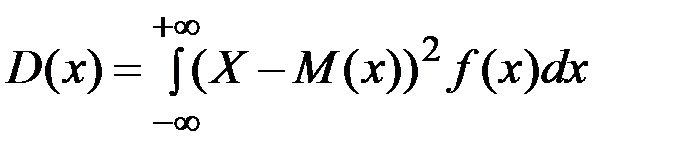 . (2.30)
. (2.30)
6. Среднее квадратическое отклонение
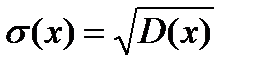 . (2.31)
. (2.31)
7. Коэффициент вариации:
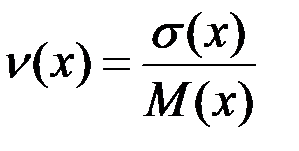 , (2.32)
, (2.32)
n (х) < 0,1 – малое значение коэффициента;
n (х) = 0,1…0,33 – среднее значение коэффициента;
n (х) > 0,33 – большое значение коэффициента.
Свойства математического ожидания:
М(ах) = аМ(х), а = const;
М(а + х) = а + М(х);
М(х ± у) = М(х)± М(у);
М(ху) = М(х) × М(у);
М(х2) = (М(х))2 + D(х).
Свойства дисперсии:
D(ах) = а2D(х), а = const;
D(а + х) = D(х);
D(х ± у) = D(х)± D(у);
D(х2) = М(х4) – [(М(х))2 + d(х)2].
Пример 2.1. Закон распределения случайной величины задан в виде таблицы:
| Х | |||
| Р(х) | 0,3 | 0,5 | 0,2 |
Определить числовые характеристики случайных величин.
Решение:
М(х) = 1 · 0,3 + 2 · 0,5 + 5 · 0,2 = 2,3
D(х) = (1 – 2,3)2· 0,3 + (2 – 2,3)2 · 0,5 + (5 – 2,3)2 · 0,2 » 2
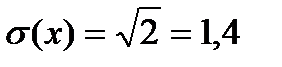
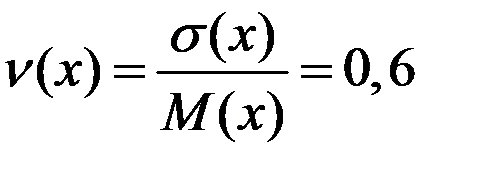 .
.
Пример 2.2. Функция распределения имеет вид:
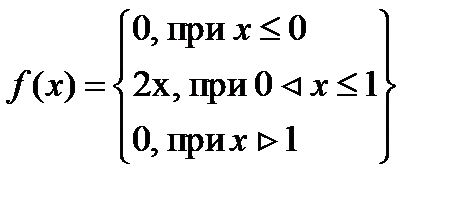
Оценить количественно, что вероятность примет значение из диапазона (0,5; 1). Какова вероятность попадания случайной величины в диапазон (0,5; 1) при условии, что событие не появится?
Решение:
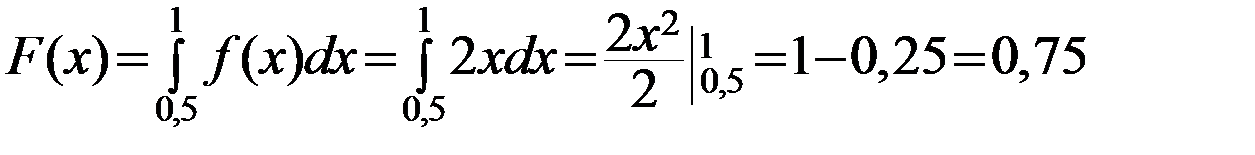 ,
,
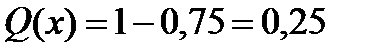 .
.
Контрольные вопросы и задачи
1. Почему надёжность необходимо рассматривать в вероятностном аспекте?
2. Как можно подсчитать вероятность безотказной работы через число отказавших объектов и общее число объектов?
3. Какими способами задаются случайные величины?
4. Перечислите и поясните основные теоремы вероятности.
5. Назовите следствия основных теорем теории вероятностей.
6. Закон распределения случайной величины задан в виде таблицы:
| х | –2 | |||
| Р(х) | 0,2 | 0,1 | 0,4 | 0,3 |
Известно, что M(x) = 0.
Найти D(x),  (x), ν(x), M(x2).
(x), ν(x), M(x2).
7. Функция распределения имеет вид:
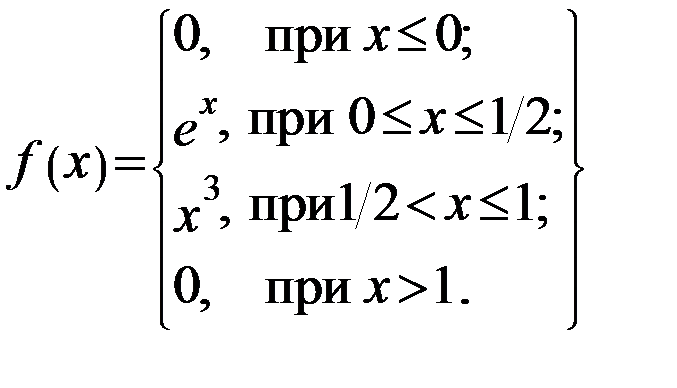
Найти вероятность того, что вероятность примет значение из диапазона
(1/3; 2/3).
8. Прибор работает в двух режимах: «1» и «2». Режим «1» наблюдается в 60 % случаев, режим «2» – в 40 % случаев за время работы T. В режиме «1» прибор отказывает с вероятностью, равной 0,3, а в режиме «2» – с вероятностью 0,5. Определить вероятность отказа прибора за время T. Ответ: 0,38.
9. Прибор (рис. 2.5) состоит из трех блоков, которые независимо друг от друга могут отказать. Отказ каждого из блоков приводит к отказу всего прибора. Вероятность того, что за время T работы прибора откажет первый блок, равна 0,15, второй – 0,25, третий – 0,1. Найти вероятность того, что время T прибор проработает безотказно.
Ответ: 0,57375.

Рис. 2.5. Схема прибора
10. Прибор (рис. 2.6) состоит из двух блоков, дублирующих друг друга. Вероятность того, что время T каждый из блоков проработает безотказно, равна 0,9. Отказ прибора произойдет при отказе обоих блоков. Найти вероятность того, что время T прибор проработает безотказно.
Ответ: 0,99.

Рис. 2.6. Схема прибора
Дата добавления: 2016-02-16; просмотров: 1254;
