Предварительные сведения
Безотказность и другие свойства надёжности проявляются через случайные величины: наработку до отказа (наработку между отказами) и количество отказов за заданное время. Поэтому количественными характеристиками здесь выступают вероятностные переменные.
Наработка – продолжительность (объём) работы объекта. Измеряется в любых неубывающих величинах (единица времени, число циклов нагружений, километры пробега и т. п.). Объект может работать непрерывно (с учётом перерывов на ремонт) или с перерывами, не зависящими от технического состояния (в этом случае различают непрерывную и суммарную наработки).
Появление отказов не предопределено заранее, т. е. случайно, поэтому теория надежности основана на математическом аппарате теории вероятностей и математической статистики.
Для оценки надёжности проводятся эксплуатационные испытания значительного числа N элементов в течение времени t. Пусть к концу испытаний остается Nр работоспособных элементов и n отказавших.
Тогда относительное количество отказов:
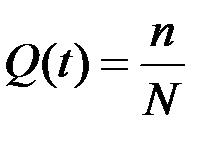 . (3.1)
. (3.1)
Вероятность безотказной работы оценивается относительным количеством работоспособных элементов:
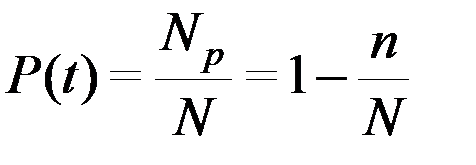 . (3.2)
. (3.2)
Вероятность безотказной работы (ВБР) означает, что в пределах заданной наработки отказ объекта не возникнет.
Так как безотказная работа и отказ – взаимно противоположные события, то сумма их вероятностей равна единице:
P(T) + Q(t) = 1,
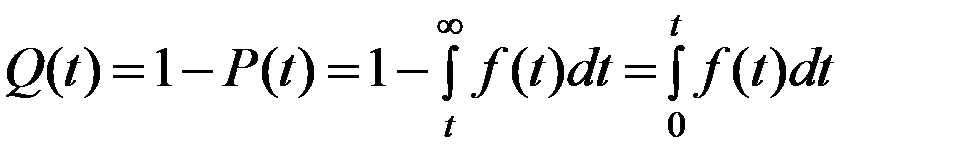 =F(t).
=F(t).
F(t) есть интегральная функция распределения случайной наработки t.
Так как события, заключающиеся в том, что наступил или не наступил отказ к моменту наработки t, являются противоположными, то нетрудно убедиться, что P(t) является убывающей, а Q(t) – возрастающей функцией наработки (рис. 3.1).
| P(t) Q(t) |
| P(t) |
| Q(t) |
| t |
Рис. 3.1. Изображения функций P(t) и Q(t)
Действительно: а) в момент начала испытаний (t = 0) число работоспособных объектов равно общему их числу N(t) = N(0) = N,
а число отказавших – n(t) = n(0) = 0,
поэтому P(t) = P(0) = 1,а Q(t) = Q(0) = 0;
б) при наработке t, возрастающей до бесконечности (t  ∞), все объекты, поставленные на испытания, откажут, т. е.
∞), все объекты, поставленные на испытания, откажут, т. е.
N(∞) = 0, а n(∞) = N, поэтому P(t) = P(∞) = 0,а Q(t) = Q(∞) = 1.
Вероятность безотказной работы есть количественная мера того, что случайная величина наработки до отказа T окажется не меньше некоторой заданной наработки t, если t ≥0:
P(t) = P{T ≥ t}. (3.3)
Очевидно, что Q(t) является функцией распределения случайной величины T и представляет собой вероятность того, что наработка до отказа окажется меньше некоторой заданной наработки t:
Q(t) = P{T < t}. (3.4)
Пример 3.1. Найти P(t) в интервале наработки [t, t + ∆t] при условии, что объект безотказно проработал до начала t интервала.
Решение:
Вероятность определяется посредством использования теоремы умножения вероятностей и выделения следующих событий:
A = {безотказная работа объекта до момента t};
B = {безотказная работа объекта в интервале ∆t};
C = A·B = {безотказная работа объекта до момента t + ∆t}.
Очевидно, что P(C) = P(A·B) = P(A)·P(B/A), поскольку события A и B будут зависимыми.
Условная вероятность P(B/A)представляет P(t, t + ∆t) в интервале
[t, t + ∆t], поэтому
P(B / A) = P(t, t + ∆t) = P(C) / P(A) = P(t + ∆t) / P(t). (3.5)
Q(t) в интервале наработки [t, t + ∆t], с учётом (3.5), равна:
Q(t, t + ∆t) = 1 – P(t, t + ∆t) = [P(t ) – P(t + ∆t)] / P(t). (3.6)
Все изделия являются либо невосстанавливаемыми, либо восстанавливаемыми.
Дата добавления: 2016-02-16; просмотров: 735;
