Табличный закон распределения
| X | х1 | х2 | х3 | … | хn |
| P(X) | P(x1) | P(x2) | P(х3) | … | P(хn) |
| Рис. 2.1. Многоугольник распределения |
Для непрерывных величин табличный способ не применяется. Непрерывные случайные величины задаются функцией распределения (рис. 2.2):
F(x) = P(x1,¥).
Рис. 2.2. Функция распределения непрерывной случайной величины
Функция распределения имеет ряд свойств:
1) она является неубывающей функцией ее аргумента, т. е. при х2 > х1
F(х2) > F(x1);
2) на минус бесконечности функция распределения равна нулю
;
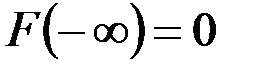3) на плюс бесконечности функция распределения равна единице
.
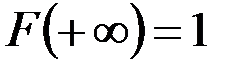Плотность распределения («плотность вероятности») – первая производная от функции распределения. Другие названия: «дифференциальная функция распределения», «дифференциальный закон распределения».
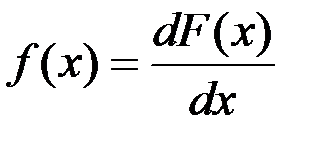. (2.25)
Плотность распределения изображается кривой распределения и показывает, как по оси абсцисс распределяются массы, т. е. кривая проходит через концы абсцисс значений «линейной плотности» (рис. 2.3).
Свойства плотности распределения:
1) плотность распределения – функция неотрицательная:
;
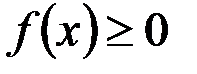2) интеграл в бесконечных пределах от плотности распределения равен единице:
.
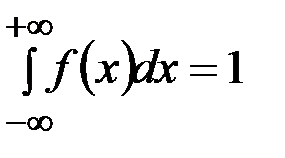Рис. 2.3. Плотность распределения
Согласно свойству 2, функция распределения в интервале от 0 до х1
(рис. 2.4) определяется как интеграл плотности распределения
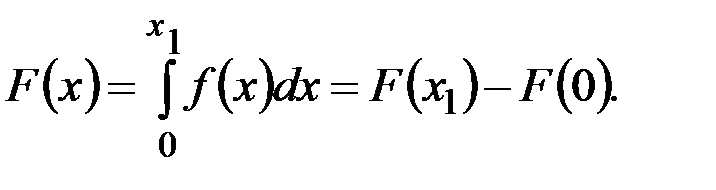(2.26)
Рис. 2.4. Определение функции распределения
В ряде случаев бывает достаточно указать числовые характеристики.
Дата добавления: 2016-02-16; просмотров: 881;