Показатели безотказности невосстанавливаемых объектов

Невосстанавливаемыми называются такие объекты, для которых восстановление работоспособного состояния не предусмотрено в нормативно-техни­ческой и (или) конструкторской (проектной) документации [7].

Если происходит отказ такого изделия, то выполняемая операция будет сорвана, и ее необходи­мо начинать вновь в том случае, если возможно устранение отказа.

К таким изделиям относятся как изделия однократного действия (ракеты, управляемые снаряды, искусственные спутники Земли, усилители системы под­водной межконтинентальной связи и т. п.), так и изделия многократного действия (некоторые системы навигацион­ного комплекса судового оборудования, системы ПВО, системы управления воздушным движением, системы управления химическими, металлургическими и другими ответственными производственными процессами и т. д.).

Для невосстанавливаемых объектов применяется понятие наработка до отказа (он же является и последним отказом).

В расчетах пользуются средней наработкой до отказа, определяемой в [7] как математическое ожидание наработки объекта до первого отказа.

Средняя наработка до отказа Т₁ вычисляется по формуле

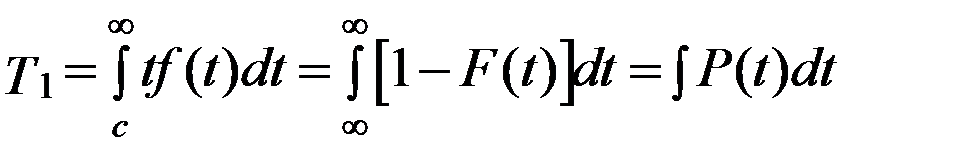, (3.7)

где F(t) – функция распределения наработки до отказа;

Р(t) – вероятность безотказной работы;

f(t) – плотность распределения наработки до отказа.

Статистически средняя наработка до отказа определяется по формуле

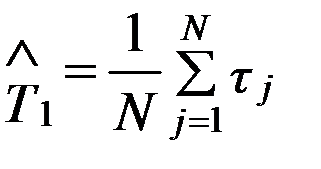, (3.8)

где N – число работоспособных объектов при t = 0;

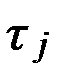– наработка до первого отказа каждого из объектов.

Длядифференцируемых функций распределения случайной величины определяется первая производная, называемая плотностью распределения
(законом распределения) времени работы объекта до отказа:

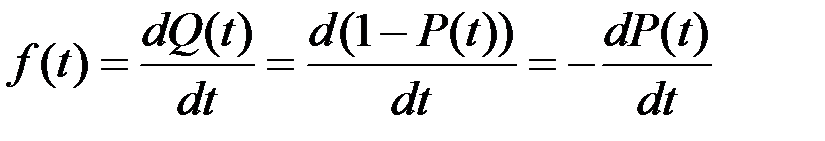. (3.9)

Другим важным показателем надежности является интенсивность отказов, котораясообщает, какая часть объектов выходит из строя в единицу времени относительно среднего числа исправно работающих объектов.

Интенсивность отказов как статистический параметр – отношение числа отказавших объектов в единицу времени к числу объектов, продолжающих безотказно работать в данный промежуток времени:

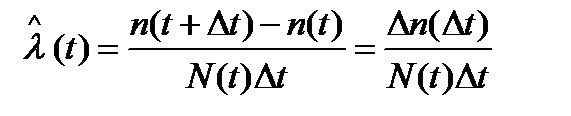, (3.10)

где Δn(Δt)– число отказавших объектов за промежуток времени от (t –Δt / 2)до (t +Δt / 2),

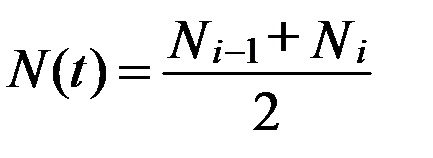, (3.11)

где N_{i – 1} – число исправно работающих объектов в начале интервала Δt;

N_i – число исправно работающих объектов в конце интервала Δt.

Интенсивность отказов как вероятностный параметр – условная плотность вероятности возникновения отказа изделия при условии, что до рассматриваемого момента времени t отказ не возник [7]:

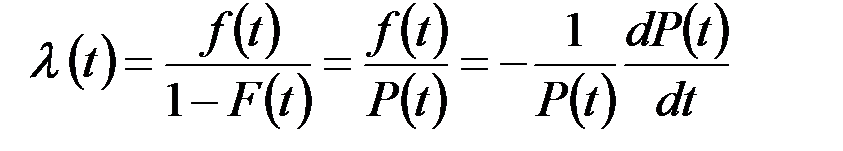, (3.12)

где функции f(t) и λ(t) измеряются в часах в минус первой степени.

При интегрировании (3.12) получается:

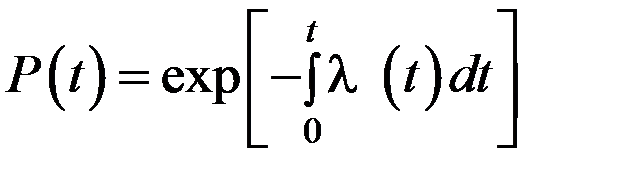. (3.13)

Величина λ(t)dt есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t], откажет в интервале [t, t + dt].

Выражение (3.12), называемое основным законом надежности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени.

В частном случае постоянства интенсивности отказов λ(t) = 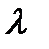= const выражение (3.12) преобразуется в известное в теории вероятностей экспоненциальное распределение

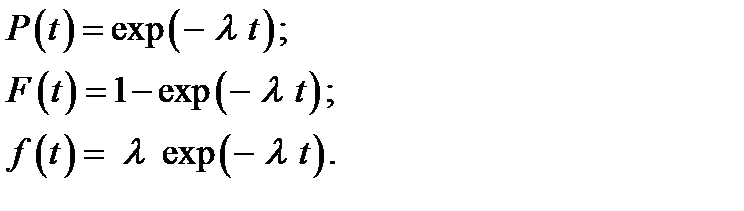
Таким образом, для невосстанавливаемых объектов применяют показатели Р(t), Т₁, f(t), λ(t).

F(t) – функция распределения наработки до отказа;

Р(t) – вероятность безотказной работы;

f(t) – плотность распределения наработки до отказа.