Показатели безотказности восстанавливаемых объектов
Восстанавливаемыми называются изделия, которые в процессе выполнения своих функций допускают ремонт. Если произойдет отказ такого изделия, то он вызовет прекращение функционирования изделия только на период устранения отказа. К таким изделиям относятся: телевизор, агрегат питания, станок, автомобиль, трактор и т. п.
Величина λ(t)dt есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t], откажет в интервале [t, t + dt].
Для восстанавливаемых объектов применяется понятие наработка на отказ (наработка между двумя соседними во времени отказами). После каждого отказа производится восстановление работоспособного состояния.
Характеристикой безотказности случайной наработки Т является математическое ожидание, которое называется средней наработкой на отказ (между отказами) [7].
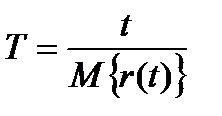 , (3.14)
, (3.14)
где t – суммарная наработка; r(t) – число отказов, наступивших в течение этой наработки; М{r(t)} – математическое ожидание этого числа. В общем случае средняя наработка на отказ оказывается функцией t.
Статистическая оценка средней наработки на отказ Тесть величина, рассчитываемая по формуле
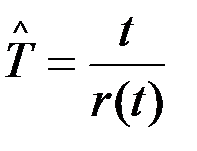 . (3.15)
. (3.15)
В отличие от формулы (3.9) здесь r(t) – число отказов, фактически происшедших за суммарную наработку t.
Статистическая вероятность отказов
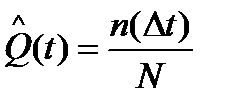 , (3.16)
, (3.16)
где n(Dt) – количество отказов;
N – число взятых на испытания объектов.
Статистическая частота отказов
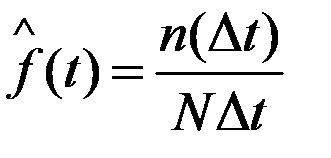 , (3.17)
, (3.17)
где Dt – данный интервал времени.
Параметры работоспособности:
– вероятность безотказной работы Р(t);
– средняя наработка на отказ Т;
– параметр потока отказов μ(t);
– среднее время восстановления ТВ.
Параметр потока отказовμ(t)есть отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую его наработку к значению этой наработки: 
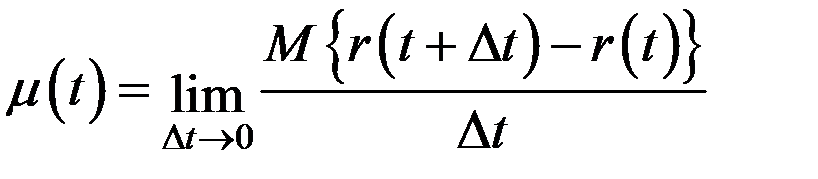 , (3.18)
, (3.18)
где 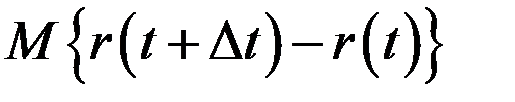 – математическое ожидание;
– математическое ожидание; 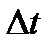 – малый отрезок наработки; r(t) –число отказов, наступивших от начального момента времени до достижения наработки t;
– малый отрезок наработки; r(t) –число отказов, наступивших от начального момента времени до достижения наработки t; 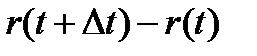 –число отказов на отрезке
–число отказов на отрезке 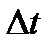 .
.
При расчетах и обработке экспериментальных данных применяют осредненный параметр потока отказов
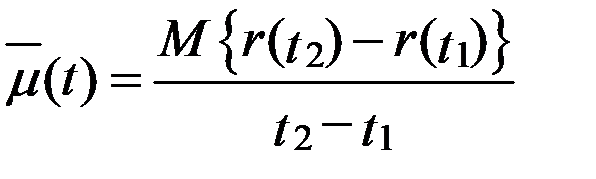 ,(3.19)
,(3.19)
здесь 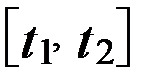 – конечный отрезок времени, на котором определяется число отказов, причем
– конечный отрезок времени, на котором определяется число отказов, причем 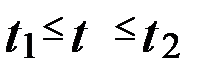 . Для стационарного потока отказов параметры, определяемые по формулам, не зависят от t .
. Для стационарного потока отказов параметры, определяемые по формулам, не зависят от t .
Cтатистическая оценка параметра потока отказов делается по формуле, которая аналогична формуле (3.19):
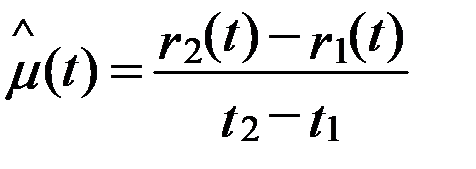 . (3.20)
. (3.20)
Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта. Отказы объектов возникают в случайные моменты времени, и в течение заданного периода эксплуатации наблюдается поток отказов.
Существует множество математических моделей потоков отказов. Наиболее часто при решении задач надежности электроустановок используют простейший поток отказов – пуассоновский поток. Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствия последствия.
Стационарность случайного процесса (времени возникновения отказов) означает, что на любом промежутке времени Δti вероятность возникновения n отказов зависит только от n и величины промежутка Δti, но не зависит от сдвига Δti по оси времени. Следовательно, при 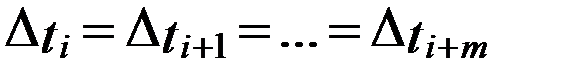 вероятность появления n отказов по всем интервалам составит
вероятность появления n отказов по всем интервалам составит
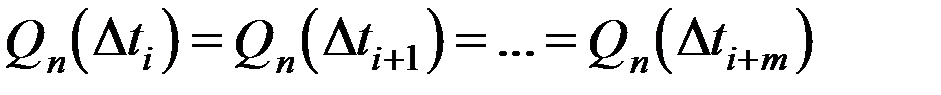 . (3.21)
. (3.21)
Ординарностьслучайного процесса означает, что отказы являются событиями случайными и независимыми. Ординарность потока означает невозможность появления в один и тот же момент времени более одного отказа, т. е.
при n >1 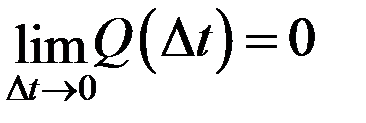 . (3.22)
. (3.22)
Отсутствие последствия означает, что вероятность наступления n отказов в течение промежутка Δti не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.
Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно, и если старение элементов отсутствует
(l = const), то поток отказов в системе можно считать простейшим.
Случайные события, образующие простейший поток, распределены по закону Пуассона:
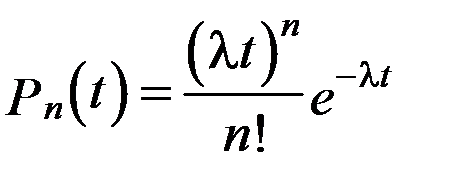 при
при  nі ³ 0, (3.23)
nі ³ 0, (3.23)
где 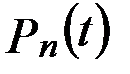 – вероятность возникновения в течение времени t ровно n событий (отказов); l – параметр распределения, совпадающий с параметром потока событий.
– вероятность возникновения в течение времени t ровно n событий (отказов); l – параметр распределения, совпадающий с параметром потока событий.
Если в выражении (3.23) принять n = 0, то получится 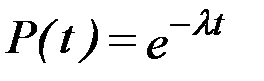 – вероятность безотказной работы объекта за время t при интенсивности отказов
– вероятность безотказной работы объекта за время t при интенсивности отказов
l = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику l = const, то, придавая объекту восстанавливаемость, следует написать μ(t) = const; l = μ .
Это свойство широко используется в расчётах надёжности ремонтируемых устройств. Например, важнейшие показатели надежности оборудования электроустановок даются в предположении, что потоки отказов и восстановлений являются простейшими, когда 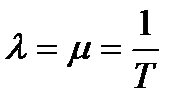 и, соответственно,
и, соответственно,
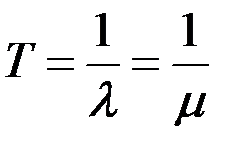 . (3.24)
. (3.24)
Среднее время восстановления 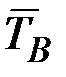 :
:
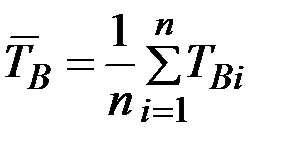 , (3.25)
, (3.25)
где n – число отказов объекта;
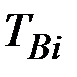 – время, затраченное на отыскание и устранение одного отказа.
– время, затраченное на отыскание и устранение одного отказа.
Функция распределения:
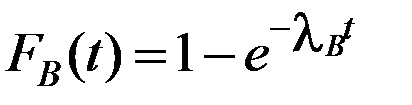 , (3.26)
, (3.26)
где 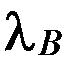 – интенсивность восстановления работоспособности объекта; характеризует среднее число восстановлений ремонтируемого объекта в единицу времени,
– интенсивность восстановления работоспособности объекта; характеризует среднее число восстановлений ремонтируемого объекта в единицу времени,
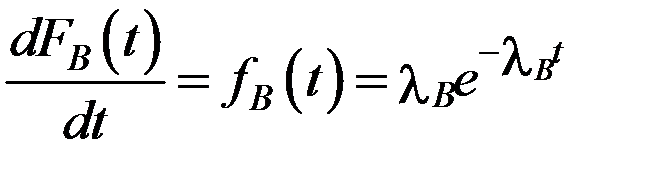 . (3.27)
. (3.27)
Интенсивность восстановления работоспособности объекта:
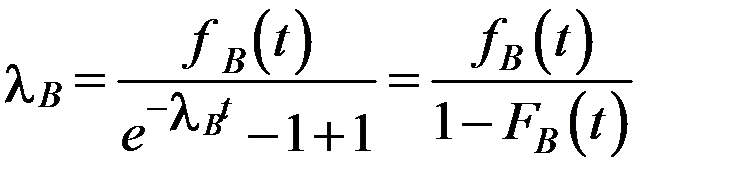 , (3.28)
, (3.28)
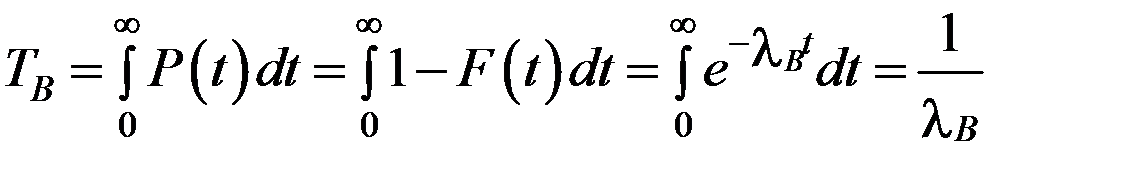 , (3.29)
, (3.29)
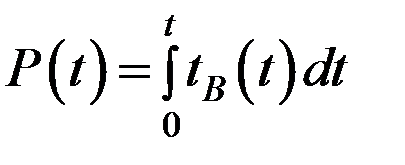 , (3.30)
, (3.30)
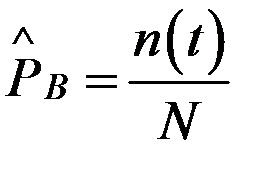 , (3.31)
, (3.31)
где n(t) – число восстановленных за время t объектов;
N – общее число отказавших объектов.
Вероятность безотказной работы восстанавливаемого объекта:
Pr (t) – количественная мера того, что объект в заданный момент времени будет работоспособен.
Событие А: объект работоспособен до момента времени t и работоспособен на участке времени Dt. Выражение для события А:
Р(t, t + Dt) = Р(t)Р(Dt) = Р(t)е –lt.
Событие В: объект вышел из строя к моменту времени t, но был восстановлен за период D t. Выражение для события В:
Р(t, t + Dt) = (1 – Р(t))(1 – е –lDt),
Р(t, t + Dt) = P(t) е –lDt + (1 – P(t))(1 – е –lDt) . (3.32)
Согласно формулам (3.9)–(3.13)
е –lDt = 1 – lВDt
преобразуется к виду:
1 – е –lDt = lВDt,
P(t, t + Dt) = P(t)(1 – lDt) + (1 – Р(t)),
lВ Dt = 1,
1 = P(t) – P(t)lDt + lВ Dt – P(t) lВ Dt,
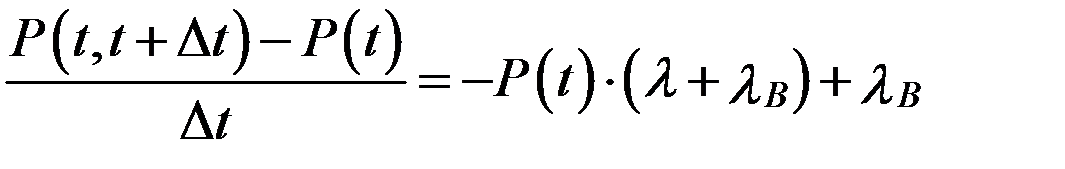 ,
,
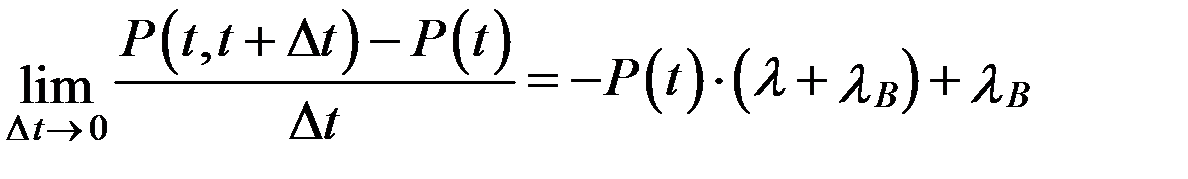 ,
,
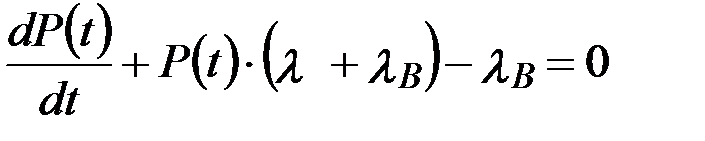 .
.
Решение этого дифференциального уравнения имеет вид:
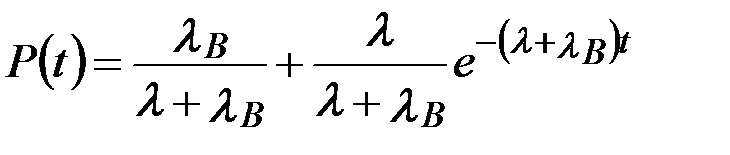 . (3.33)
. (3.33)
Изображение функции Pr(t) восстанавливаемого изделия и функции P(t) невосстанавливаемого изделия представлено на рис. 3.2.
Надёжность восстанавливаемого Pr(t) изделия всегда выше надёжности невосстанавливаемого изделия P(t).
Пример 3.2. В результате наблюдения за работой редуктора было зарегистрировано 8 отказов, наработки ti составляют в сутках:18, 9, 14, 27, 16, 8, 14, 22.
P(t)
| Pr (t) |
| P(t) |
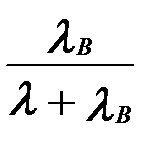
рис. 3.2. графики функции Pr(t)и P(t)
Определить наработку на отказ 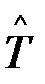 и вероятность его безотказной работы в пределах наработки Dt = 20 ч.
и вероятность его безотказной работы в пределах наработки Dt = 20 ч.
Решение:
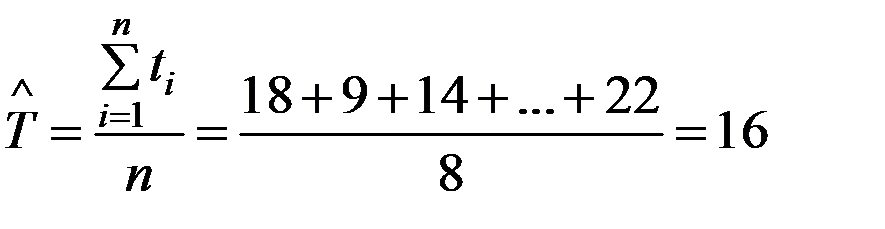 суток,
суток,
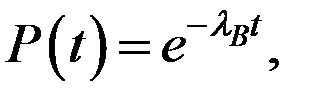
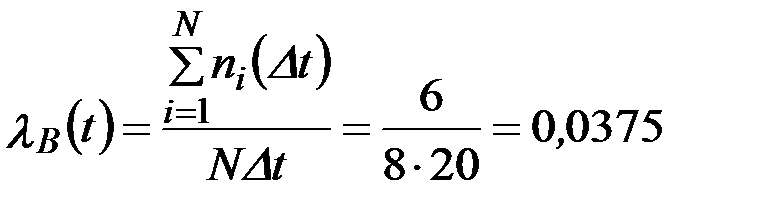 ,
,
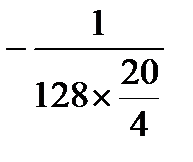
|
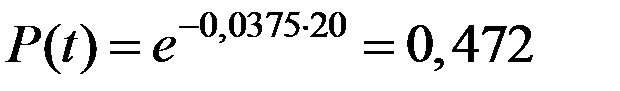 .
.
Дата добавления: 2016-02-16; просмотров: 5307;
