Теорема о повторении опытов

Следствием правил сложения и умножения вероятностей является теорема о повторении опытов (схема Бернулли):опыты считаются независимыми, если вероятность того или иного исхода каждого из них не зависит от того, какие исходы имели другие опыты.

Пусть в некотором опыте вероятность события А равна P(А) = p, а вероятность того, что оно не произойдет, P( 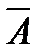) = q, причём

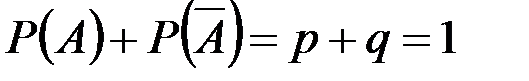. (2.18)

Если проводится n независимых опытов, в каждом из которых событие А появляется с вероятностью p, то вероятность того, что в данной серии опытов событие А появляется ровно m раз, определяется по выражению

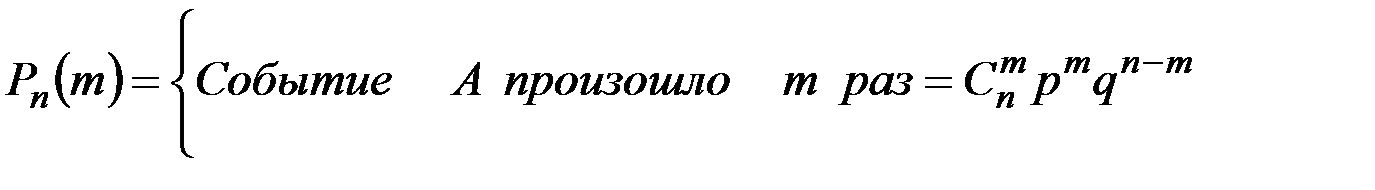, (2.19)

где 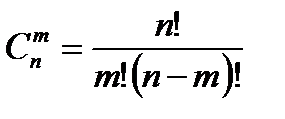– биномиальный коэффициент. (2.20)

Например, вероятность отсутствия ошибки чтения 32-разрядного слова в формате ЭВМ, представляющего комбинацию 0 и 1, при вероятности ошибки чтения двоичного числа p = 10^–3 составляет по (2.8) при m = 0, :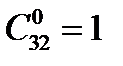

.

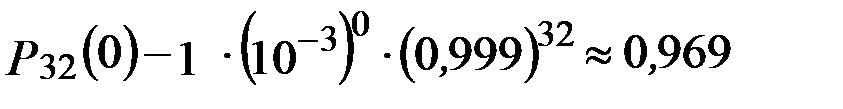При больших m вычисление биномиальных коэффициентов C_n^m и возведение в большие степени p и q связано со значительными трудностями, поэтому целесообразно применять упрощенные способы расчётов. Приближение,
называемое теоремой Муавра – Лапласа, используется, если npq>>1,
а |m – np|<(npq)^0,5, в таком случае выражение (2.19) записывается:

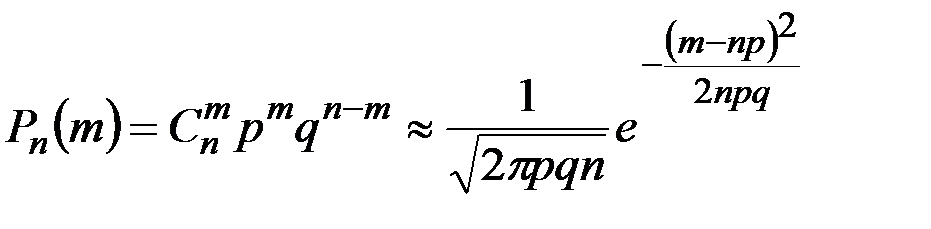. (2.21)