Ранг неопределенности модели

С целью однозначного и неизбыточного представления моделей систем управления на разных этапах исследования введено понятие «ранг наопределенности» 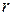причинно-следственных отношений моделей, которое отражает степень информативности (полноту знаний) о системе и внешней среде, т.е. топологии (структуре) ситсемы, характере и видах операторов связей элементов системы и внешней среды, значениях их параметров.

В результате представления моделей 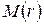на соответствующем ранге снимается неопределенность о модели:

на топологическом – неопределенность о топологии;

на структурно-операторном – неопределенность о структурах операторов;

на параметрическом – неопределенность о параметрах.

Исходным этапом получения математического описания системы, например, в виде частной модели 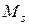, является выделение множества переменных 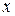. Указанное множество называют моделью системы нулевого ранга неопределенности ( 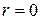) и обозначают как 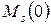. Геометрически данная модель представляет собой совокупность точек (вершин), т.е. нуль-граф. Нулевой ранг можно назвать элементным.

4.3. Модели первого (топологического) ранга
неопределенности

Теоретико-множественный (теоретико-графовый) способ представления. Множество переменных 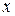и заданное на этом множестве полинарное ( 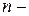е, многоместное), в частности, бинарное (двуместное), отношение 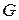называют моделью первого ранга неопределенности 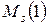. Отношение 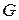представляет собой множество из неупорядоченных между собой переменных 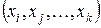, в частности, двоек 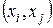. При однородности всех индексированных переменных достаточно указывать только их индексы: , .

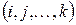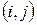В общем случае, топологическим (структурным) представлением 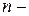го отношения является гиперграф.

Неориентированным гиперграфом (просто гиперграфом) называют тройку множеств 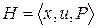, в которой 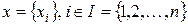– множество вершин; 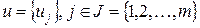– множество ребер; 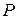– инцидентор (двуместный предикат), определенный на множестве всех пар 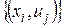. Вершины и ребра составляют элементы гиперграфа 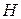(предикат – это условие, т.е логическая функция, принимающая значения «истина-1» или «ложь-0»):

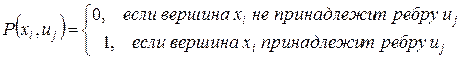
Указанное представление является теоретико-множественным (теоретико-графовым) способом задания модели систем первого ранга неопределенности.

Вершина 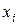и ребро 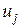инцидентны, если .

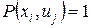Вводят понятия множества вершин, инцидентных данному ребру (область инциденции ребра), и множества ребер, инцидентных данной вершине (область инциденции вершины). Мощности указанных множеств называют степенями, т.е. степенями ребер и степенями вершин.

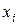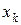Две вершины и смежны в гиперграфе 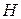, если существует ребро, которому они инцидентны, т.е. соединены этим ребром.

Два ребра смежные в гиперграфе 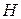, если существует вершина, инцидентная этим ребрам, т.е. связанная с этими ребрами.

Другой способ теоретико-множественного представления гиперграфа – через множество 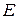ребер гиперграфа, заданных в виде подмножеств множества вершин: 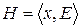. Другими словами, каждой вершине сопоставляется элемент множества 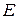, представляющий собой подмножество вершин, связанных ребрами с данной вершиной.

Причинно-следственная модель системы первого ранга неопределенности 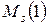характеризуется отношением 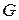, представляющим собой множество из 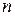упорядоченных переменных 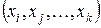, в частности, упорядоченных двоек 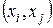, где первая по порядку следования переменная соответствует следствию, а остальные – причинам. Каждая упорядоченная последовательность переменных – элемент связей, – есть кортеж.

Модель 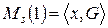задает топологию системы. Число связей, т.е. мощность множества 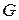, обозначают 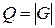. С учетом причинно-следственных связей модель 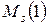представляет собой ориентированный граф с 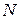вершинами и 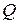дугами.

На рисунке 4.1 показан пример ориентированного графа (орграфа), который может описывать топологию линейной стационарной системы.

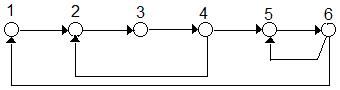
Рисунок 4.1 – Орграф линейной стационарной системы

Топология системы в виде бинарных отношений имеет следующее описание: ; ; .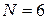

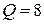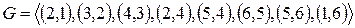С использованием полинарных отношений топология имеет описание: ; ; .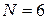

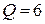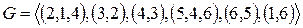Другим способом теоретико-множественного описания причинно-следственной модели 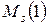в виде орграфа является задание множества переменных 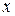и отображения 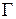, т.е. 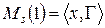. Отображение 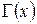, называемых множеством правых инциденций, показывает, причиной изменения каких переменных является переменная 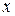. Для системы, изображенной на рисунке 4.1, описание имеет вид: ; ; ; ; ; .

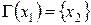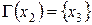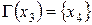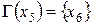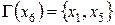Еще один способ – через использование обратного отображения 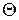, показывающего, следствием изменения каких переменных является 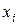. Множество 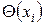называю множеством левых инциденций. Для рассматриваемого примера имеем: ; ; ; ; ; .

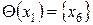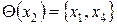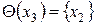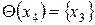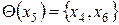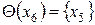Алгебраический способ представления. Данный способ представления опирается на использовании матриц смежности, инциденций, изоморфности.

Матрица смежности 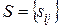– квадратная матрица размерности 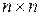, где 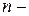размерность вектора 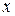. Элемент 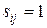, если существует связь (дуга) между переменной-причиной 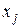и переменной-следствием 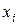. Несвязанным переменным соответствует .

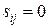Для примера, показанного на рисунке 4.1, матрица смежности имеет вид:

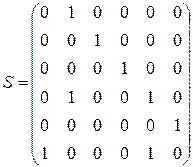
Недостатком матриц смежности является их «разреженность», достоинством – возможность определения важных характеристик графа (наличие петель и контуров, изолированных элементов, тупиков и т.д) путем вычисления степеней матрицы смежности. В частности, для определения контура из 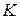вершин, необходимо вычислить 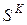. Тогда на главной диагонали полученной матрицы будут ненулевые элементы в тех позициях, которые соответствуют вершинам, лежащим на контуре. Для определения всех контуров необходимо вычислить все степени матрицы смежности Эти операции используются, в частности, при анализе так называемых «информационных» графов, используемых при описании документооборота на предприятиях.

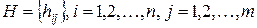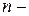Матрица инциденций , где число вершин, 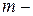число дуг, является прямоугольной матрицей, состоящей из элементов -1, 0, 1. При этом 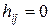, если элементы не связаны между собой; 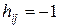, если дуга, соединяющая 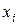с 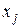, исходит из 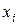; 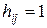, если дуга, соединяющая 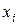с 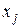, приходит в 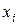. Для примера рисунка 4.1. матрица инциденций имеет вид:

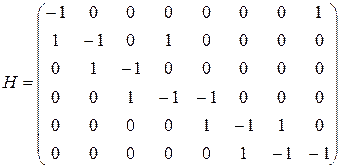
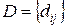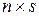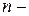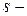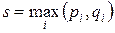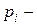Матрица изоморфности имеет размер , где число вершин, а максимальная степень вершин, определяемая по формуле , где число входящих дуг, 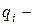число исходящих дуг. В 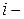ю строку матрицы 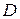со знаком «+» вписывают номера дуг, входящих в 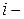ю вершину, а со знаком «–» вписывают номера исходящих дуг. Название объясняется тем, что с помощью данной матрицы с точностью до изоморфизма (геометрического образа) можно восстановить диаграмму графа. В сравнении с матрицами смежности и инциденций матрица изоморфности наиболее компактная. Для примера рисунка 4.1. матрица изоморфности имеет вид:

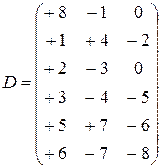
Здесь использована следующая нумерация дуг: 1 – (2, 1); 2 – (3, 1); 3 – (4,1); 5 – (5, 4); 6 – (6, 5); 7 – (5, 6); 8 – (1, 6), где при обозначении дуг на первом месте указана вершина-приемник, на втором месте – вершина-источник.

Пример определения контуров. Для графа рисунка 4.1 имеют место три контура: (2, 3, 4), (5, 6), (1,2,3,4,5,6). Перемножая матрицы 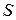, получаем:

, ,

. ,

.

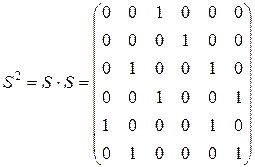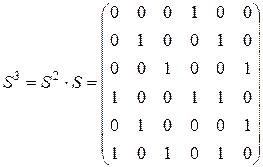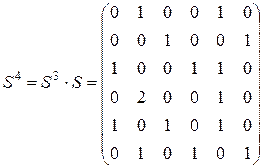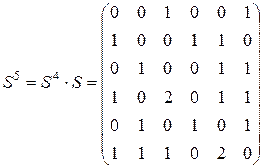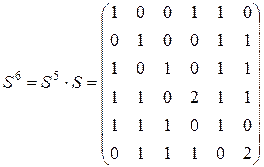Из 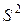следует наличие контура из двух вершин (5, 6). Из 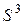следует наличие контура из трех вершин (2, 3, 4). Из 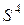следует, что контуров длиной 4 нет, т.к. здесь на диагонали для контура длиной 4 должны быть 4 ненулевых элемента, а есть всего два. Из 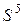также следует, что контуров длиной 5 нет. Из 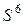следует наличие контура (1, 2, 3, 4, 5, 6). Сравнивая полученные результаты с рисунком 4.1, видим, что изображенный граф содержит именно эти контуры.

5. МОДЕЛИ СИСТЕМ УПРАВЛЕНИЯ ВТОРОГО и ТРЕТЬЕГО
РАНГОВ НЕОПРЕДЕЛЕННОСТИ

Дальнейшее раскрытие неопределенности моделей систем управления возможно при установлении структуры операторов связи между переменными – модель второго (структурно-операторного) ранга неопределенности. Данные модели определяют систему с точностью до параметров.

Существуют несколько форм представления таких моделей, рассмотренных ниже.

5.1. Представление моделей в форме пространства
состояний

Достоинством данной формы является однородный вид и возможность использования матричных операций. Традиционно данный аппарат применяется для описания линейных систем, однако его можно обобщить и на нелинейные системы. Характерными особенностями данного описания являются: 1) задание модели системы в виде системы дифференциальных уравнений первого порядка, разрешенных относительно производной, т.е. нормальной формы Коши; 2) учет входных воздействий в виде отдельного (для линейных или аффинных систем) векторно-матричного члена в правых частях дифференциальных уравнений; 3) учет выхода системы в виде отдельного векторно-матричного соотношения.

Модель состояния имеет вид:

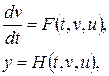(5.1)

где 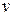– вектор состояния размерности 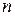; 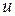– вектор входов размерности 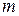; 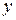– вектор выходов размерности .

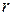Модель (5.1) нестационарная ввиду явной зависимости от текущего времени 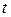. Для нелинейных систем, когда вектор-функци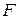и и 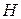нелинейные, нестационарные системы легко сводятся к стационарным введением дополнительного дифференциального уравнения вида 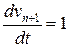, в результате чего размерность 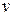увеличивается на единицу, а модель приобретает стационарный вид

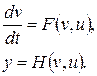(5.2)

Линейная модель состояния – частный случай (5.1), когда:

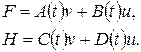(5.3)

Линейную нестационарную систему (5.3) также можно свести к стационарной указанным выше способом, однако в общем случае эта замена приведет к появлению нелинейностей. По этой причине в линейной теории управления стационарные и нестационарные системы анализируются и синтезируются различными методами.