Примеры нетехнических задач.

Модель гонки вооружений (линейная).Изменения количества вооружений 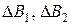у каждой из двух стран за время 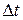определяется выражениями:

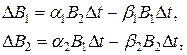
где неотрицательные 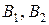– объемы вооружений; коэффициенты 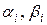– соответственно скорости наращивания и старения вооружений. Поделив на 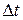и устремив 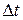к нулю, получим систему дифференциальных уравнений:

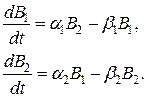
В модели можно учесть также не зависящие от количества вооружений и времени уровни недоверия 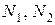в виде дополнительных слагаемых:

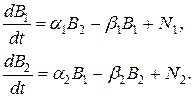
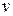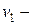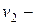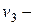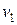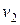Модель распространения эпидемического заболевания.Пусть исследуемое население , подвергшееся эпидемии, можно разделить на три группы: здоровые люди, восприимчивые к болезни; заболевшие люди; невосприимчивые к заболеванию люди. Предполагается, что и не контактируют. Предполагается, что 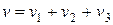. Группу людей 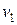пополняют здоровые люди 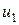, а группу больных 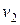– заболевшие 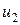. Тогда модель имеет вид:

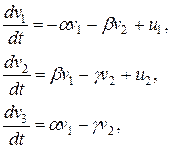
где 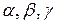– положительные коэффициенты пропорциональности, характеризующие интенсивности изменения соответствующих групп; 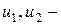скорости появления новых людей, соответственно восприимчивых к заболеванию и инфицированных.

Более точная нелинейная модель имеет вид:

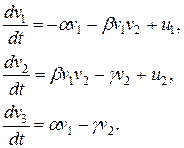
Здесь учтено взаимодействие групп 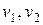, если указанные группы контактируют друг с другом.

Модель обмена потребительскими стоимостями (товарного обмена). Рассматривается экономическая модель обмена различных товаров 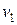и 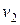двух производителей, испытывающих взаимные потребности в товарах друг друга. Нелинейная модель обмена имеет вид:

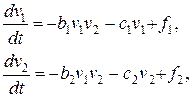
где 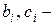неотрицательные коэффициенты пропорциональности; положительные 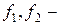величины, характеризующие производство; члены с произведениями являются обменными (контактными) и описывают рыночный обмен. Отношение 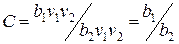является меновой стоимостью обмена. Члены 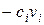учитывают физический и моральный износ товаров.

Приравнивая производные нулю, получаем систему нелинейных уравнений рыночного равновесия.