Входные воздействия

Вектор входов часто разделяют на вектор возмущающих воздействий и вектор управляющих воздействий. Возмущающие же воздействия иногда разделяют на известные заранее и неизвестные заранее на всем интервале времени работы системы. Кроме того, возмущающие воздействия делят на детерминированные (неслучайные) и случайные. Случайными могут быть не только изменяющиеся во времени воздействия (случайные процессы), но и начальные (граничные) условия, а также параметры в виде случайных величин. Их, а также случайные события, называют случайными факторами. Как правило, случайные процессы задаются в виде законов распределений сечений и корреляционных функций (спектральных плотностей). Случайные величины задаются законами распределения. Случайные события задаются распределениями вероятностей. При компьютерном моделировании случайных факторов используются известные методы.

5.3. Разнообразие форм представления моделей «вход-состояние-выход»

Наряду с представлениями (5.1) – (5.3), рассматривают различные частные случаи.

Отдельно выделяют класс так называемых аффинных систем (систем с линейно входящим вектором входов):

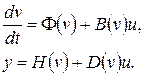(5.4)

Смысл выделения аффинных систем в том, что для них разработаны специальные методы синтеза. Существует возможность приведения систем вида (5.2) к аффинным системам путем введения дифференциальных уравнений для вектор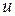а вида 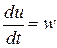и соответствующего расширения размерности вектора 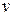: 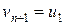, , 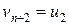…, 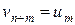. Новая система будет иметь вид (5.4) с векторами 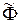и 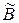вместо 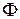и 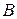, расширенным на 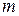компонент вектором 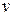и 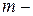мерным вектором входов 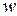вместо 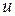. При этом:

, .

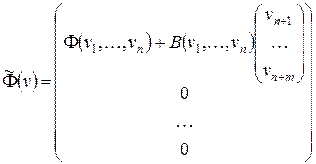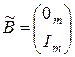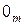В приведенной выше системе слева показаны нулевых компонент вектора , справа нулевая и единичная 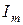квадратные матрицы размерности 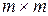. Такая замена формально делает новую систему аффинной, однако возникает проблема подобия, поскольку новые входы поступают на дополнительные интегрирующие звенья, чего не было в исходной системе. Тем не менее, для методов управления, построенных для аффинных систем, это позволяет расширить область их применения.

Еще один класс систем, для которых разработаны отдельные методы – билинейные системы вида:

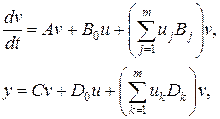
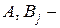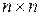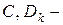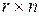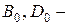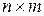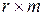где числовые матрицы размера ; числовые матрицы размера ; числовые матрицы размера и соответственно.

Системы без входных воздействий называются однородными:

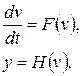(5.5)

К однородным можно отнести и системы с известными на всем интервале времени работы системы внешними воздействиями.

При постановке задач управления важны также начальные или краевые условия, а также интервал времени работы системы.

5.4. Общие и частные решения дифференциальных
уравнений

На уровне моделей второго ранга, где параметры не заданы, можно говорить только об аналитических решениях и условиях их существования и единственности. В общем случае дифференциальные уравнения могут иметь несколько решений, проходящих через одну точку.

Что касается аналитических решений, то они бывают общие и частные. Обозначим некоторое частное решение системы (5.2) 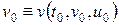, где индексом «0» обозначены начальное время и начальные значения переменной состояния и входа. Смысл тождества в том, что при подстановке начальных условий в решение получается начальное условие. Если в решении 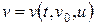вместо вектора начальных условий 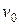подставить произвольный вектор 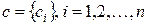, получим общее решение. Общее решение – это семейство решений, содержащее в себе все без исключения решения однородного дифференциального уравнения. Эти решения отличаются друг от друга лишь значениями произвольных постоянных. Методологически можно поступать по-разному. Первый способ заключается в первоначальном поиске общего решения, используя неопределенные интегралы, а затем из него определять частное решение, удовлетворяющее заданным начальным условиям. Во втором способе вначале ищут частное решения, используя определенные интегралы, а затем начальные условия заменяются произвольными постоянными.

Пример.

Рассмотрим простейшее дифференциальное уравнение

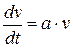. (5.6)

Найдем его общее решение через неопределенный интеграл методом разделяющихся переменных. Имеем следующую цепочку выкладок, где для упрощения последующих преобразований произвольная постоянная для неопределенного интеграла взята в виде :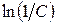

, , , , ,

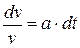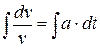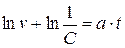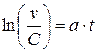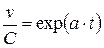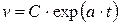. (5.7)

Выражение (5.7) представляет собой общее решение уравнения (5.6). Найдем из (5.7) частное решение, соответствующее начальному условию 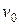в момент 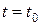. Имеем: 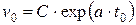; 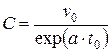, откуда следует частное решение:

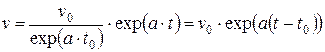. (5.8)

Для получения частного решения вторым способом выполним следующие действия:

; ; ; ;

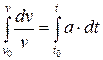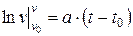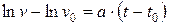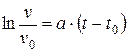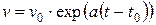. (5.9)

Для получения общего решения из частного (5.9) выполним следующие действия: 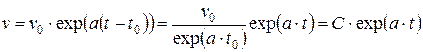. Здесь в произвольную постоянную включено не только 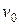, но и член, связанный с 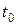. Получено общее решение, совпадающее с (5.7).