Первый интеграл и его свойства
Для моделей, представленных системой однородных дифференциальных уравнений
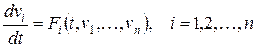 (5.12)
(5.12)
вводится понятие первого интеграла.
Первым интегралом системы (5.12) называют функцию 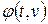 , определенную и непрерывную вместе со своими частными производными, если при подстановке в нее произвольного решения
, определенную и непрерывную вместе со своими частными производными, если при подстановке в нее произвольного решения 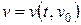 получается постоянная относительно времени
получается постоянная относительно времени 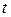 величина. Такая функция является инвариантом во времени. Неизменность первых интегралов во времени порождается различными законами сохранения, зависящими от координаты и ее первой производной.
величина. Такая функция является инвариантом во времени. Неизменность первых интегралов во времени порождается различными законами сохранения, зависящими от координаты и ее первой производной.
Исходя из определения 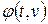 , эта функция должна удовлетворять условию:
, эта функция должна удовлетворять условию:
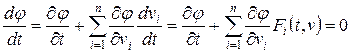 . (5.13)
. (5.13)
Примером первого интеграла является гамильтониан (3.23) для консервативных систем, свидетельствующий о сохранении полной энергии такой системы.
У системы может быть несколько независимых первых интегралов, но не больше 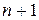 . Количество же зависимых первых интегралов неограниченно.
. Количество же зависимых первых интегралов неограниченно.
Первые интегралы используются, во-первых, для понижения порядка системы дифференциальных уравнений. Во-вторых, с помощью первых интегралов существенно повышают точность решений, если известно, что движение системы принадлежит первому интегралу.
В общем случае нахождение первых интегралов представляет собой непростую задачу. Проще решается обратная задача – конструирование желаемых первых интегралов за счет выбора подходящего управления.
Средством получения первых интегралов является уравнение (5.13), а также теорема Якоби-Пуассона, на основе которой формируются новые первые интегралы.
5.7. Представление моделей в форме системы
дифференциальных уравнений различных порядков
В достаточно общем виде модель второго ранга неопределенности может быть представлена системой в неявной форме записи:
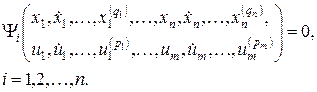 (5.14)
(5.14)
где 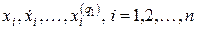 – физические переменные системы и их производные, включая как внутренние, так и выходные переменные;
– физические переменные системы и их производные, включая как внутренние, так и выходные переменные; 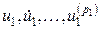 ,
, 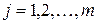 – внешние воздействия, приложенные к системе, и их производные, включая задающие, возмущающие и управляющие воздействия.
– внешние воздействия, приложенные к системе, и их производные, включая задающие, возмущающие и управляющие воздействия.
В случае решения задачи Коши задают временной интервал работы системы и начальные условия:
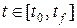 ,
, 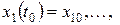
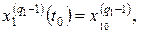
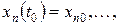
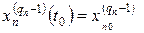
Для некоторых переменных и воздействий описание может не содержать их производных, так что 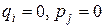 . При этом отдельные уравнения будут не дифференциальными, а конечными. Приведенное описание соответствует представлению модели в терминах «вхо-выход».
. При этом отдельные уравнения будут не дифференциальными, а конечными. Приведенное описание соответствует представлению модели в терминах «вхо-выход».
Общий порядок системы определяется суммой порядков старших производных каждой переменной, т.е. 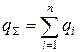 .
.
Модели вида (5.14) обычно имеют место на стадии первичного описания. При переходе же к стадии компьютерного моделирования эти модели требуется преобразовывать к той форме, для которой существуют процедуры численного интегрирования. В большинстве случаев такой формой является нормальная форма Коши. Для нее разработаны численные методы и процедуры, реализованные в известных математических пакетах. Поэтому исследователю необходимо уметь переходить от формы (5.14) к нормальной форме.
Переход от дифференциального уравнения высокого порядка к системе уравнений первого порядка.Без потери в общности рассмотрим частный случай (5.14), зависящий только от одной переменной и одного внешнего воздействия:
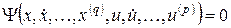 . (5.15)
. (5.15)
Применяют разные способы перехода. Рассмотрим два таких способа на примере линейного стационарного уравнения 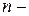 го порядка (здесь роль
го порядка (здесь роль 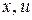 выполняют переменные
выполняют переменные 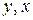 соответственно:
соответственно:
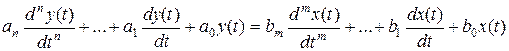 . (5.16)
. (5.16)
В физически реализуемых звеньях 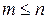 .
.
Первый способ. Если правая часть уравнения не содержит производных входного сигнала 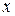 либо они известны из других уравнений (когда
либо они известны из других уравнений (когда 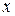 – выход другого звена структурной схемы), то для (5.16) переход производится с помощью алгоритма
– выход другого звена структурной схемы), то для (5.16) переход производится с помощью алгоритма
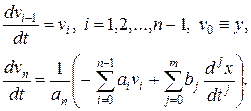 (5.17)
(5.17)
Так, для случая n=2, m=1 эквивалентная система имеет вид:
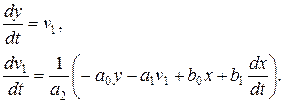
Для (5.15) необходимо предварительно выразить старшую производную (такие уравнения называют разрешенными относительно старшей производной:
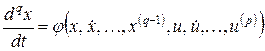 . (5.18)
. (5.18)
При таком способе перехода в системе остаются производные входного воздействия, которые во многих случаях неизвестны (когда 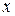 – возмущающее воздействие) либо не существуют (например, в моменты скачков ступенчатого воздействия). Достоинство же метода в том, что он, в принципе, применим к любым системам вида (5.14), (5.15), если они разрешимы относительно старшей производной.
– возмущающее воздействие) либо не существуют (например, в моменты скачков ступенчатого воздействия). Достоинство же метода в том, что он, в принципе, применим к любым системам вида (5.14), (5.15), если они разрешимы относительно старшей производной.
Для линейных стационарных систем используется другой способ перехода к нормальной системе, так называемой канонической ее форме.
Второй способ (переход к канонической форме). Алгоритм перехода к канонической форме следующий:
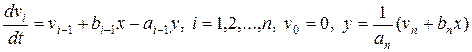 . (5.19)
. (5.19)
Здесь предполагается, что 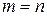 , а для всех
, а для всех 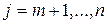 коэффициенты
коэффициенты 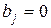 .
.
Для рассматриваемого случая каноническая система имеет вид
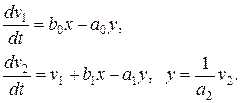
Дата добавления: 2016-04-02; просмотров: 1273;
