Пример технической задачи.

Имеется трубопроводная сеть, граф которой изображен на рисунке 3.1.

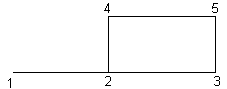
Рисунок 3.1 – Граф трубопроводной сети

Предполагается, что геометрические уровни вершин 1, 2, 3 z1=z2=z3=0, уровни вершин 4, 5 z4=z5=5м. В вершинах 1 и 3 имеются напорные насосы. Трубы 2-4 и 3-5 - цилиндрические емкости высотой 5м, - предназначены для долговременного хранения питьевой воды. Емкость 2-4 имеет диаметр 3м, емкость 3-5 - диаметр 5м. Остальные трубы диаметром 1м и длиной 10м каждая предназначены для подвода воды (труба 1-2) и соединения емкостей (трубы 2-3 и 4-5). В вершине 5 предполагается свободный выход воды через трубу, которая в рассматриваемую систему не входит. Целью управления является прокачка воды через емкости с помощью насосов таким образом, чтобы вода в каждой емкости обновлялась каждые два часа.

Модель данной системы без учета процессов перемешивания строится на основе уравнений Бернулли для неустановившегося напорного движения несжимаемой жидкости в предположении абсолютной жесткости стенок труб. Система уравнений Бернулли для рассматриваемой задачи имеет вид

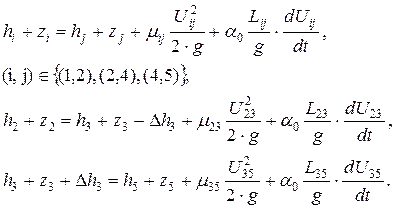(3.28)

Здесь 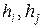– пьезометрические напоры в i-й и j-й вершинах сети; 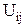– средняя скорость потока в трубе i-j; 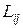–длина трубы i-j; 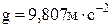– ускорение свободного падения, 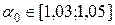–коэффициент коррекции количества движения. Параметр 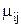определяется формулой Кармана-Никурадзе

,

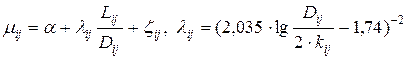где 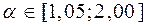– коэффициент коррекции скорости, учитывающий степень турбулентности потока (большие значения соответствуют меньшей турбулентности); 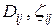– диаметр и коэффициент местного сопротивления(i-j)-й трубы. Коэффициент сопротивления 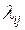(коэффициент Дарси) рассчитывается по приведенной выше формуле Кармана-Никурадзе для шероховатых труб, в которой 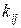– средняя высота бугорков шероховатости. Член 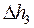отражает наличие насоса в месте соединения трубы (2,3) и емкости (3,5). Так как насос, нагнетая воду в емкость, одновременно отсасывает ее из трубы (2,3) и наоборот, указанный член входит в уравнения для (2,3) и (3,5) с разными знаками. Пьезометрический напор 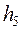при свободном выходе потока из вершины 5 нулевой.

Наряду с (3.28), в динамическую модель входят уравнения сохранения потока в виде системы уравнений для расходов во внутренних вершинах сети.

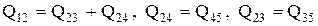. (3.29)

Для вершины 5 уравнение сохранения не записываем, так как из нее имеется свободный выход потока.

Расходы 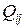связаны со средними скоростями 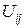соотношением

,

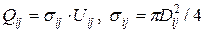где 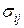– площадь поперечного сечения i-j-й трубы.

Последняя группа уравнений модели – уравнения для уровней воды в емкостях

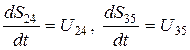. (3.30)

Указанные уровни отображают не уровни заполнения емкостей (они на протяжении всего времени работы системы предполагаются заполненными), а местоположения выделенных частиц воды, по которым можно судить о степени обновления воды в емкостях.

Целью прокачки является достижение уровням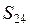и и 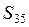значения Sz=5м за заданное время 7200с.

В рассмотренном примере видны элементы рассматриваемого метода – приход воды в точку 1, уход воды из точки 5. Источников и стоков нет, поскольку подпитка и утечки не предполагаются. Балансовые соотношения в чистом виде – уравнения (3.28), (3.29). Однако и уравнения (3.30) также рассматривают как балансовые (см. уравнения (3.28) с производными в правых частях).

Другими техническими задачами, где данный метод широко применяется, являются задачи в области электротехники, где в качестве основы для составления балансовых соотношений используется закон Кирхгоффа и эквивалентные схемы (схемы замещения).