Логистические модели (из Википедии).

Модель Мальтуса. Согласно модели, предложенной Мальтусом, скорость роста пропорциональна текущему размеру популяции, то есть описывается дифференциальным уравнением:

,

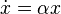где 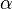— некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция 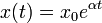. Если рождаемость превосходит смертность ( 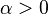), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов.

Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста.

Логистическое уравнение, также известное как уравнение Ферхюльста (по имени впервые сформулировавшего его бельгийского математика), изначально появилось при рассмотрении модели роста численности населения. Исходные предположения для вывода уравнения при рассмотрении популяционной динамики выглядят следующим образом:

• скорость размножения популяции пропорциональна её текущей численности, при прочих равных условиях;
• скорость размножения популяции пропорциональна количеству доступных ресурсов, при прочих равных условиях. Таким образом, второй член уравнения отражает конкуренцию за ресурсы, которая ограничивает рост популяции.

Обозначая через 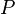численность популяции (в экологии часто используется обозначение 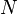), а время — 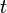, модель сводится к дифференциальному уравнению:

,

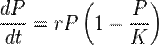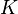где параметр характеризует скорость роста (размножения), а — поддерживающую ёмкость среды (то есть, максимально возможную численность популяции). Исходя из названия коэффициентов, в экологии часто различают две стратегии поведения видов:

• -стратегия предполагает бурное размножение и короткую продолжительность жизни особей
• а 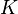-стратегия — низкий темп размножения и долгую жизнь.

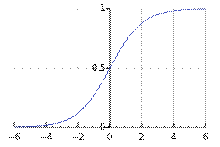
Рисунок 3.2 – Логистическая кривая для K=1 и P₀=0,5

Точным решением уравнения (где 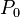— начальная численность популяции) является логистическая функция, S-образная кривая, (логистическая кривая):

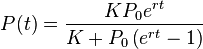
где

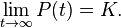
Ясно, что в ситуации «достаточного объёма ресурсов», то есть пока P(t) много меньше K, логистическая функция поначалу растёт приблизительно экспоненциально:

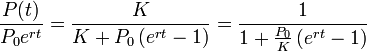
Аналогично, при «исчерпании ресурсов» (t → ∞) разность 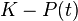экспоненциально убывает с таким же показателем. Почему Ферхюльст назвал уравнение логистическим, остается неизвестным. В 1924 году Раймонд Перл применил уравнение для описания автокаталитических реакций.

Модель промышленного рыболовства.Это модель естественного изменения численности рыбы в замкнутом водоеме и в основном подчиняется тем же законам, что и модель Ферхюльста. В отличие от модели Мальтуса полагается, что параметр роста-убыли 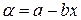, а уравнение баланса имеет вид:

,

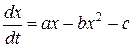т.е. тем самым в ней посредством члена 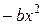отражается факт ухудшения условий существования (конкурентной борьбы за пищу, болезней) с ростом численности популяции. Коэффициент 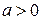называется коэффициентом естественного прироста, а коэффициент 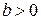– коэффициентом внутривидовой конкуренции. Коэффициент 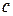означает установленную квоту на темп отлова рыбы.

Модель хищник-жертва. Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов 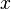, число лис 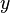. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки-Вольтерры:

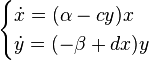
Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерры-Лотки ответа не дает: здесь требуются дополнительные исследования.

4. ПРЕДСТАВЛЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
СИСТЕМ УПРАВЛЕНИЯ