Представление моделей систем в форме уравнений Гамильтона. Консервативные и диссипативные системы

В данном формализме кинетическая энергия представляется как функция обобщенных моментов 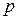и обобщенных координат 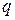, где

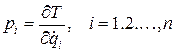. (3.14)

Функцию 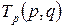называют функцией Гамильтона для кинетической энергии или кинетической энергией в гамильтоновых или канонических координатах 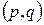. Для единообразия обозначений далее кинетическую энергию, выраженную через 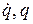, будем записывать как .

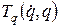Поскольку энергия не зависит от того, через какие координаты она выражается, справедливо равенство

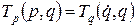. (3.15)

Далее будем учитывать, что обобщенная скорость зависит от обобщенных моментов и координат, т.е. .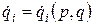

Продифференцируем (3.15) по 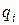. С учетом того, что 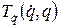зависит от конкретного 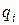явно и неявно (через 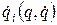, получим следующее:

.

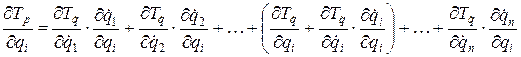С учетом (3.14) последнее соотношение перепишем в виде:

.

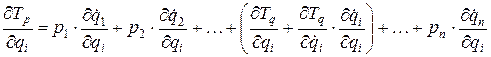Кинетическую энергию для стационарной системы можно выразить через обобщенные скорости, используя теорему Эйлера об однородных функциях, которая для используемых здесь обозначений имеет вид:

,

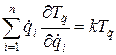где 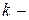порядок однородности. Поскольку кинетическая энергия - квадратическая функция, 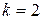(см. (3.3), получаем следующее выражение.

.

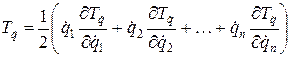С учетом (3.14):

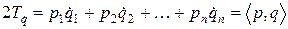, (3.16)

е.е. скалярное произведение.

Вычислим частную производную по 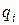от последнего выражения:

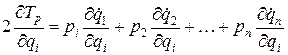. (3.17)

В результате преобразования уравнений получаем:

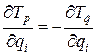. (3.18)

Частная производная по 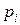от (3.15) определяется выражением:

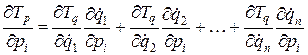. (3.19)

Дифференцируя по 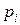выражение (3.16), получим уравнение:

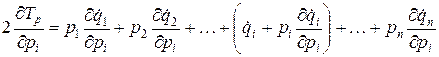. (3.20)

Вычтем из выражения (3.20) выражение (3.19). В результате получим:

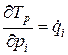. (3.21)

Используя равенства (3.18) и (3.21), уравнения движения Лагранжа

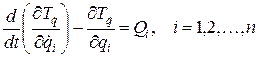
могут быть представлены в виде системы уравнений:

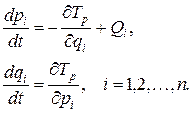(3.22)

Систему уравнений (3.22) называют уравнениями Гамильтона. Эти уравнения в частных производных связывают кинетическую энергию с обобщенными координатами и моментами, а также, в общем случае, с обобщенными силами.

Функцию, выражающую полную энергию системы, которая в консервативных системах остается неизменной, через обобщенные координаты 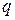и импульсы 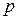, называют функцией Гамильтона или гамильтонианом:

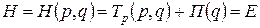. (3.23)

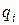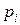В результате дифференцирования (3.23) по и имеем:

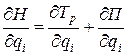, (3.24)

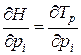. (3.25)

Полученные формулы устанвливают связь между гамильтонианом и энергиями (кинетической и потенциальной) в дифференциальной форме. При подстановке (3.24), (3.25) в (3.22) с учетом (3.11) получаем систему уравнений:

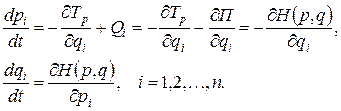(3.26)

Система уравнений (3.26) получила название канонических уравнений Гамильтона.

Для консервативной системы гамильтониан не зависит от времени. В самом деле, после подстановки (3.26) в выражение для производной гамильтониана по времени имеем:

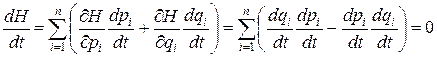. (3.27)

Это справедливо в том случае, когда гамильтониан не зависит от времени явно, т.е. в том случае, когда полная энергия в системе не изменяется во времени.

Явная зависимость от времени появляется тогда, когда система либо теряет, либо получает энергию (полная энергия системы зависит от времени). В этом случае изменение за счет 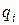и 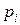по-прежнему равно нулю, а изменение 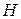полностью определяется частной производной .

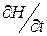Поведение любой динамической системы подчиняется принципу сжатия-расширения фазового пространства.

Из уравнений (3.26) следует:

,

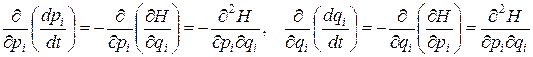откуда

.

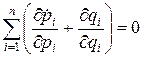Обозначим 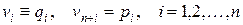. В новых обозначениях последнее равенство имеет вид:

.

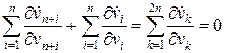Обозначив правые части объединенной системы (2.36) как 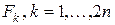, последнее равенство перепишем в виде:

.

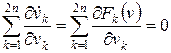Данное соотношение означает, что дивергенция векторного поля скоростей равна нулю, т.е.

.

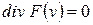Дивергенция (скалярная величина) характеризует скорость сжатия или расширения фазового объема. Еще один физический смысл ненулевой дивергенции – наличие источников или стоков (в данном случае – энергии). Т.е., если система консервативная, у нее нет потерь энергии или ее притока извне, а фазовый объем не меняется.

Динамически системы с изменяющимся во времени запасом энергии называют неконсервативными. Системы с уменьшающимся запасом энергии (например, из-за трения или рассеяния) называются диссипативными. В противном случае имеем системы с отрицательной диссипацией.

Для консервативных систем имеет место обратимость уравнений динамики, а их размерность является четной.

Для диссипативных систем фазовый объем со временем сжимается, в пределе, до нуля. При этом фазовые координаты при 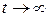стремятся к некоторому «аттрактору», т.е. компактному множеству нулевого объема (например, в трехмерном пространстве аттрактором может быть кривая, лежащая в плоскости).

Некоторые сведения об аттракторах:

1. Система, находящаяся в начальном состоянии вне аттрактора, с течением времени попадают на аттрактор.

2. В результате притяжения к аттрактору происходит своеобразная «потеря памяти» диссипативной системы о ее начальных условиях.

3. Размерность аттрактора всегда меньше размерности фазового пространства.

4. Возможно существование нескольких аттракторов со своими областями притяжения.